题目内容
12.已知函数f(x)=$\frac{1}{3}$x3-ax2+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.(1)求a,b的值;
(2)求函数f(x)在区间[-2,4]上的最大值.
分析 (1)根据导数的几何意义求出函数在x=1处的导数,从而得到切线的斜率,建立等式关系,再根据切点在函数图象建立等式关系,解方程组即可求出a和b,从而得到函数f(x)的解析式;
(2)先求出f′(x)=0的值,根据极值与最值的求解方法,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值.
解答 解:(1)f′(x)=x2-2ax,
∵(1,f(1))在x+y-3=0上,
∴y=-x+3=f(1)=$\frac{1}{3}$-a+b=2①,
f′(1)=-1=1-2a②,
由①②解得:a=1,b=$\frac{8}{3}$;
(2)∵f(x)=$\frac{1}{3}$x3-x2+$\frac{8}{3}$,
∴f′(x)=x2-2x,
由f′(x)=0可知x=0和x=2是f(x)的极值点,所以有
| x | (-∞,0) | 0 | (0,2) | 2 | (2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
∵f(0)=$\frac{8}{3}$,f(2)=$\frac{4}{3}$,f(-2)=-4,f(4)=8,
∴在区间[-2,4]上的最大值为8.
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数求闭区间上函数的最值等基础题知识,考查运算求解能力,考查数形结合思想.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
2.已知对数函数 f(x)=logax(a>0,且a≠1)在区间[2,4]上的最大值与最小值之积为2,则a=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$或 2 | C. | $2\sqrt{2}$ | D. | 2 |
3.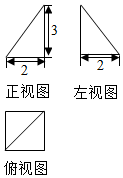 已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
 已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )| A. | $\frac{4}{3}$cm3 | B. | $\frac{8}{3}$cm3 | C. | 2cm3 | D. | 4cm3 |
20.等差败列{an}的前n项和为Sn,若a3+a16=10,则S18=( )
| A. | 50 | B. | 90 | C. | 100 | D. | 190 |
17.如果直线l1:x+ax+1=0和直线l2:ax+y+1=0垂直,则实数a的值为( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 0 |
4.已知圆C1:x2+y2=4和圆2:(x-a)2+y2=4,其中a是在区间(0,6)上任意取得一个实数,那么圆C1和圆C2相交且公共弦长小于2$\sqrt{3}$的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |