题目内容

10．函数f（x）=sinx-$\frac{2}{5π}$x零点的个数是（　　）
A．4B．6C．7D．8

分析 作出y=sinx与y=$\frac{2}{5π}x$的函数图象，根据图象的交点个数和对称性判断．

解答 解：令f（x）=0得sinx=$\frac{2}{5π}$x，
作出y=sinx与y=$\frac{2}{5π}x$的在（0，+∞）上的函数图象，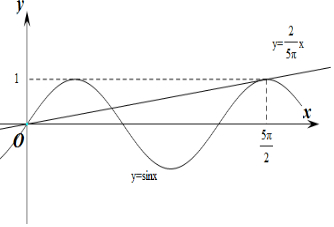

由图象可知y=sinx与y=$\frac{2}{5π}$x在（0，+∞）上有3个交点，
又y=sinx与y=$\frac{2}{5π}$x都是奇函数，且都经过原点，
故两图象在（-∞，0）上有3个交点，且原点是两函数图象的一个交点，
∴两函数在R上共有7个交点，即f（x）有7个零点．
故选C．

点评 本题考查了函数零点与函数图象的关系，属于中档题．

练习册系列答案
相关题目
14．已知定义在R上的函数$f（x）=\frac{1}{3}a{x^3}+{x^2}+ax+1$既有极大值又有极小值，则实数a的取值范围是（　　）
A．（-∞，-1）∪（1，+∞）B．[-1，0）∪（0，1]C．（-1，1）D．（-1，0）∪（0，1）
15．若数列{an}，{bn}的通项公式分别是an=（-1）2017•a，bn=2+$\frac{{{{（-1）}^{n+2018}}}}{n}且{a_n}＜{b_n}$对任意n∈N*恒成立，则常数a的取值范围是[-2，1）．
12．已知函数f（x）=（x2-2x）sin（x-1）+x+1在[-1，3]上的最大值为M，最小值为m，则M+m=4．
5．对于非空集合A，B，设k（A，B）表示集合A，B中元素个数差的绝对值，若A={1，2}，B={x||x2+ax+1|=1}，且k（A，B）=1，由a的所有可能值构成的集合是S，则S中所有元素之和为（　　）
A．0B．1C．3D．4
15．已知向量$\overrightarrow{a}$，$\overrightarrow{e}$，|$\overrightarrow{e}$|=1，f（x）=|$\overrightarrow{a}-x\overrightarrow{e}$|是定义在R上的函数，
（1）若f（x）≥f（1）对所有x∈R都成立，求证：（$\overrightarrow{a}-\overrightarrow{e}$）⊥$\overrightarrow{e}$；
（2）求当x取何值时，f（x）取到最小值．
2．利用独立性检验来考虑两个分类变量X和Y是否有关系时，通过查阅下表来确定断言“X和Y有关系”的可信度．如果k＞5.024，那么就有把握认为“X和Y有关系”的百分比为97.5%．
P（K2≥k）0.500.400.250.150.10
k0.4550.7081.3232.0722.706
P（K2≥k）0.050.0250.010.0050.001
k3.8415.0246.6357.87910.828
19．如图（1），五边形PABCD是由一个正方形与一个等腰三角形拼接而成，其中∠APD=120°，AB=2，现将△PAD进行翻折，使得平面PAD⊥平面ABCD，连接PB，PC，所得四棱锥P-ABCD如图（2）所示，则四棱锥P-ABCD的外接球的表面积为（　　）
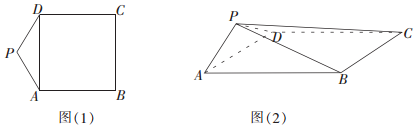
A．$\frac{14}{3}π$B．$\frac{7}{3}π$C．$\frac{28}{3}π$D．14π
20．求下列函数的导数：
（1）f（x）=（2x2+3）（3x-1）
（2）f（x）=3x•（lnx-x）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网