题目内容
19.如图(1),五边形PABCD是由一个正方形与一个等腰三角形拼接而成,其中∠APD=120°,AB=2,现将△PAD进行翻折,使得平面PAD⊥平面ABCD,连接PB,PC,所得四棱锥P-ABCD如图(2)所示,则四棱锥P-ABCD的外接球的表面积为( )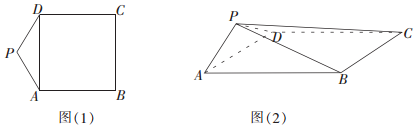
| A. | $\frac{14}{3}π$ | B. | $\frac{7}{3}π$ | C. | $\frac{28}{3}π$ | D. | 14π |
分析 将四棱锥P-ABCD补成直三棱柱PAD-MBC,则直三棱柱PAD-MBC与四棱锥P-ABCD的外接球是同一个球,故只需求出直三棱柱PAD-MBC的外接球半径即可.
解答 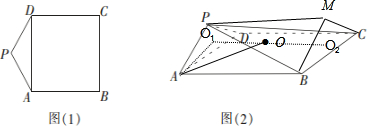 解:将四棱锥P-ABCD补成直三棱柱PAD-MBC,
解:将四棱锥P-ABCD补成直三棱柱PAD-MBC,
则直三棱柱PAD-MBC与四棱锥P-ABCD的外接球是同一个球,
故只需求出直三棱柱PAD-MBC的外接球半径即可.
如图,设直三棱柱PAD-MBC的两底的外接圆圆心分别为O1,O2,连接O1O2,
根据对称性球心为线段O1O2的中点O,
又∵底ADP的外接圆半径r,由正弦定理得$\frac{AD}{sin12{0}^{0}}=2r$,⇒r=$\frac{2}{\sqrt{3}}$,
直三棱柱PAD-MBC的外接球半径R=$\sqrt{{r}^{2}+O{{O}_{1}}^{2}}=\sqrt{\frac{7}{3}}$.
∴四棱锥P-ABCD的外接球的表面积为s=4πR2=$\frac{28}{3}π$.
故选:C.
点评 本题考查了多面体的外接球,把不易求其外接球半径的几何体转化为易求半径几何体,是解题的关键,属于中档题.

练习册系列答案
相关题目
10.函数f(x)=sinx-$\frac{2}{5π}$x零点的个数是( )
| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
7.富华中学的一个文学兴趣小组中,三位同学张博源、高家铭和刘雨恒分别从莎士比亚、雨果和曹雪芹三位名家中选择了一位进行性格研究,并且他们选择的名家各不相同.三位同学一起来找图书管理员刘老师,让刘老师猜猜他们三人各自的研究对象.刘老师猜了三句话:“①张博源研究的是莎士比亚;②刘雨恒研究的肯定不是曹雪芹;③高家铭自然不会研究莎士比亚.”很可惜,刘老师的这种猜法,只猜对了一句,据此可以推知张博源、高家铭和刘雨恒分别研究的是( )
| A. | 曹雪芹、莎士比亚、雨果 | B. | 雨果、莎士比亚、曹雪芹 | ||
| C. | 莎士比亚、雨果、曹雪芹 | D. | 曹雪芹、雨果、莎士比亚 |