题目内容
5．证明不等式$\sqrt{a+1}-\sqrt{a}＜\sqrt{a-1}-\sqrt{a-2}（{a≥2}）$所用的最适合的方法是（ ）| A． | 分析法 | B． | 综合法 | C． | 反证法 | D． | 合情推理 |
分析 从结果来找原因，或从原因推导结果，证明不等式所用的最适合的方法是分析法．
解答 解：欲证明不等式$\sqrt{a+1}-\sqrt{a}＜\sqrt{a-1}-\sqrt{a-2}（{a≥2}）$，只要证明$\sqrt{a+1}$+$\sqrt{a-2}$＜$\sqrt{a}$+$\sqrt{a-1}$，分别求出左右两式的平方，再比较出两平方式的大小．从结果来找原因，或从原因推导结果，证明不等式所用的最适合的方法是分析法．
故选D．
点评 本题考查的是分析法和综合法，解答此题的关键是熟知比较大小的方法．从求证的不等式出发，“由果索因”，逆向逐步找这个不等式成立需要具备的充分条件，分析法──通过对事物原因或结果的周密分析，从而证明论点的正确性、合理性的论证方法．也称为因果分析，属于中档题．
练习册系列答案
相关题目
13．已知函数f（x）=cosx，若存在实数x1，x2，…，xm（m≥2，m∈N）满足条件0≤x1＜x2＜…＜xm≤6π，且|f（x1）-f（x2）|+…+|f（xm-1）-f（xm）|=12，则m的最小值为（ ）
| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
20．
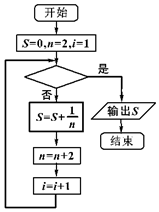如图，给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图，其中判断框内应填入的条件是（ ）
如图，给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图，其中判断框内应填入的条件是（ ）| A． | i＜11 | B． | i＞11 | C． | i＜22 | D． | i＞22 |
10．设z1，z2是复数，则下列结论中正确的是（ ）
| A． | 若${z_1}^2+{z_2}^2＞0$，则 ${z_1}^2＞-{z_2}^2$ | |
| B． | $|{{z_1}-{z_2}}|=\sqrt{{z_1}^2+{z_2}^2-4{z_1}{z_2}}$ | |
| C． | ${z_1}^2+{z_2}^2=0?{z_1}={z_2}$ | |
| D． | |z1|2=|$\overline{{z}_{1}}$|2 |