题目内容
13.若直线mx+2y+6=0与直线x+(m-1)y+m2-1=0平行,则实数m=-1.分析 利用两条直线平行,它们的斜率相等或斜率都不存在的性质求解.
解答 解:∵直线mx+2y+6=0与直线x+(m-1)y+m2-1=0平行,
∴-$\frac{m}{2}$=-$\frac{1}{m-1}$,
解得m=-1,或m=2,
当m=2时,两直线重合
故答案为:-1
点评 本题考查实数值的求法,是基础题,解题时要注意直线与直线平行的性质的合理运用.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
5.证明不等式$\sqrt{a+1}-\sqrt{a}<\sqrt{a-1}-\sqrt{a-2}({a≥2})$所用的最适合的方法是( )
| A. | 分析法 | B. | 综合法 | C. | 反证法 | D. | 合情推理 |
4.△ABC中,顶点B(3,4),C(5,2),AC边所在直线方程为x-4y+3=0,AB边上的高所在直线方程为2x+3y-16=0.
(1)求AB边所在直线的方程;
(2)求AC边的中线所在直线的方程.
(1)求AB边所在直线的方程;
(2)求AC边的中线所在直线的方程.
5.函数f(x)=2sin(3x+$\frac{π}{3}$)的最小正周期是( )
| A. | $\frac{3π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |

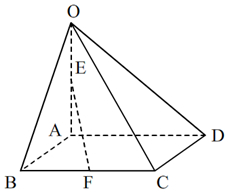 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点,
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点,