题目内容
10.设z1,z2是复数,则下列结论中正确的是( )| A. | 若${z_1}^2+{z_2}^2>0$,则 ${z_1}^2>-{z_2}^2$ | |
| B. | $|{{z_1}-{z_2}}|=\sqrt{{z_1}^2+{z_2}^2-4{z_1}{z_2}}$ | |
| C. | ${z_1}^2+{z_2}^2=0?{z_1}={z_2}$ | |
| D. | |z1|2=|$\overline{{z}_{1}}$|2 |
分析 分别举反例说明A,B,C不正确,通过计算说明D正确.
解答 解:A.错;反例:z1=2+i,z2=2-i,
B.错;反例:z1=2+i,z2=2-i,
C.错;反例:z1=1,z2=i,
D.正确,z1=a+bi,则|z1|2=a2+b2,|$\overline{{z}_{1}}$|2=a2+b2,故||z1|2=|$\overline{{z}_{1}}$|2
∴结论中正确的是:D.
故选:D.
点评 本题考查了复数的基本概念,考查了复数模的求法,是基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
1.已知函数$f(x)=4{sin^2}x+4\sqrt{3}sinxcosx+5$,若不等式f(x)≤m在$[0,\frac{π}{2}]$上有解,则实数m的最小值为( )
| A. | 5 | B. | -5 | C. | 11 | D. | -11 |
18.已知点A(0,-1)是抛物线C:x2=2py(p>0)准线上的一点,点F是抛物线C的焦点,点P在抛物线C上且满足|PF|=m|PA|,当m取最小值时,点P恰好在以原点为中心,F为焦点的双曲线上,则此双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{3}$+1 |
5.证明不等式$\sqrt{a+1}-\sqrt{a}<\sqrt{a-1}-\sqrt{a-2}({a≥2})$所用的最适合的方法是( )
| A. | 分析法 | B. | 综合法 | C. | 反证法 | D. | 合情推理 |
15.命题甲:f(x)在区间(a,b)内递增;命题乙:对任意x∈(a,b),有f'(x)>0.则甲是乙的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
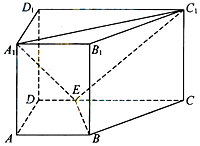 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3