题目内容
设圆满足条件:①截y轴所得的弦长为2;②圆心到直线l:x-2y=0的距离为
;③被x轴分成的两段圆弧,其弧长的比为3:1.
(1)求这个圆的方程
(2)若上述圆的圆心在第一象限,过(-1,3)点的一条光线射到x轴反射后恰好与上述圆相切,求入射光线所在的直线方程.
| ||
| 5 |
(1)求这个圆的方程
(2)若上述圆的圆心在第一象限,过(-1,3)点的一条光线射到x轴反射后恰好与上述圆相切,求入射光线所在的直线方程.
考点:直线与圆的位置关系,圆的标准方程
专题:直线与圆
分析:(1)设圆的圆心C(a,b),半径为r,则由题意可得
,求得a、b、r的值,可得要求的圆的方程.
(2)设入射光线的斜率为k,根据入射线过点(-1,3)可得入射线的方程.再根据反射定律求得反射线的方程,再根据反射线和圆(x-1)2+(y-1)2=2相切,求得k的值,可得入射线的方程.
|
(2)设入射光线的斜率为k,根据入射线过点(-1,3)可得入射线的方程.再根据反射定律求得反射线的方程,再根据反射线和圆(x-1)2+(y-1)2=2相切,求得k的值,可得入射线的方程.
解答:
解:(1)设圆的圆心C(a,b),半径为r,则由题意可得
,
求得a=b=1,r=
,或a=b=-1,r=
,
故要求的圆的方程为 (x-1)2+(y-1)2=2,或 (x+1)2+(y+1)2=2.
(2)圆心在第一象限的圆为 (x-1)2+(y-1)2=2,设入射光线的斜率为k,则反射线的斜率为-k,且入射项过点(-1,3),
故入射线的方程为 y-3=k(x+1),即 kx-y+3+k=0.
再根据点(-1,3)关于x轴的对称点(-1,-3)在反射线上,且反射线的斜率为-k,
故反射线的方程为y+3=-k(x+1),即 kx+y+3+k=0.
再根据反射线和圆 (x-1)2+(y-1)2=2相切,可得
=
,
求得k=-1,或k=-7,∴入射线的方程为x-y-2=0,或7x-y+4=0.
|
求得a=b=1,r=
| 2 |
| 2 |
故要求的圆的方程为 (x-1)2+(y-1)2=2,或 (x+1)2+(y+1)2=2.
(2)圆心在第一象限的圆为 (x-1)2+(y-1)2=2,设入射光线的斜率为k,则反射线的斜率为-k,且入射项过点(-1,3),
故入射线的方程为 y-3=k(x+1),即 kx-y+3+k=0.
再根据点(-1,3)关于x轴的对称点(-1,-3)在反射线上,且反射线的斜率为-k,
故反射线的方程为y+3=-k(x+1),即 kx+y+3+k=0.
再根据反射线和圆 (x-1)2+(y-1)2=2相切,可得
| |k+1+3+k| | ||
|
| 2 |
求得k=-1,或k=-7,∴入射线的方程为x-y-2=0,或7x-y+4=0.
点评:本题主要考查求圆的标准方程的方法,反射定理,直线和圆相切的性质,点到直线的距离公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图是一个几何体的三视图,则该几何体的表面积是( )


A、98+3
| ||
B、98+6
| ||
C、88+3
| ||
D、88+8
|
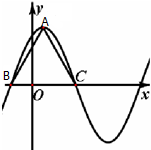 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<