题目内容
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
| 2 |
| 3 |
| 3 |
（1）求该简谐运动的函数解析式；
（2）若f（x0）=
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的求值,三角函数的图像与性质
分析：（1）利用正弦型函数的函数图象确定函数的解析式．
（2）利用三角函数的诱导关系变换直接求出函数的值．
（2）利用三角函数的诱导关系变换直接求出函数的值．
解答：
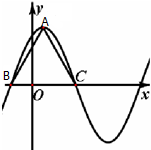
解：（1）根据函数的图象A为图象的最高点，坐标为A（
，2
）、
则：A=2
由于B、C为图象与x轴的交点，且为正三角形．
根据A=2
，△ABC为正三角形
解得：BC=4，
则：函数图象的周期T=
=8
解得：ω=
当x=
时，f(
)=2
（A＞0，ω＞0，|φ|＜
）
则：φ=
所以：f（x）=2
sin(
x+
)
（2）由（1）得：f（x）=2
sin(
x+
)
已知：x0∈(-
，
)
则：-
＜
+
＜
解得：sin(
x0+
)=
所以：cos(
x0+
)=
则：f(x0+2)=2
sin(
x0+
+
)=-2
cos(
x0+
)=-
所以函数值为：f（x0+2）=-
| 2 |
| 3 |
| 3 |
则：A=2
| 3 |
由于B、C为图象与x轴的交点，且为正三角形．
根据A=2
| 3 |
解得：BC=4，
则：函数图象的周期T=
| 2π |
| ω |
解得：ω=
| π |
| 4 |
当x=
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| π |
| 2 |
则：φ=
| π |
| 3 |
所以：f（x）=2
| 3 |
| π |
| 4 |
| π |
| 3 |
（2）由（1）得：f（x）=2
| 3 |
| π |
| 4 |
| π |
| 3 |
已知：x0∈(-
| 10 |
| 3 |
| 2 |
| 3 |
则：-
| π |
| 2 |
| πx0 |
| 4 |
| π |
| 3 |
| π |
| 2 |
解得：sin(
| π |
| 4 |
| π |
| 3 |
| 4 |
| 5 |
所以：cos(
| π |
| 4 |
| π |
| 3 |
| 3 |
| 5 |
则：f(x0+2)=2
| 3 |
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| 3 |
| π |
| 4 |
| π |
| 3 |
6
| ||
| 5 |
所以函数值为：f（x0+2）=-
6
| ||
| 5 |
点评：本题考查的知识要点：利用正弦型函数的图象确定函数的解析式，主要确定A，ω，φ的值，利用诱导公式进行函数的求值．属于基础题型．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
已知双曲线C：4x2-my2=4m（m＞0）的一条渐近线方程为2x-3y=0，则双曲线C的焦距为（ ）
A、2
| ||
| B、6 | ||
C、2
| ||
| D、4m |