题目内容
若函数f(x)=ax2+2x-1一定有零点,则实数a的取值范围是 .
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:若函数f(x)=ax2+2x-1一定有零点,则方程ax2+2x-1=0一定有实根,故a=0或a≠0且方程的判别式大于等于零.
解答:
解:若a=0,f(x)=2x-1,函数f(x)有零点;
若a≠0,则△=4+4a≥0,
解得a≥-1,
综上所述a≥-1,
故答案为:a≥-1.
若a≠0,则△=4+4a≥0,
解得a≥-1,
综上所述a≥-1,
故答案为:a≥-1.
点评:本题考查了函数的零点与方程的根之间的关系,同时考查了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
函数f(x)=sinxcosx是( )
| A、最小正周期为2π且在[0,π]内有且只有三个零点的函数 |
| B、最小正周期为2π且在[0,π]内有且只有二个零点的函数 |
| C、最小正周期为π且在[0,π]内有且只有三个零点的函数 |
| D、最小正周期为π且在[0,π]内有且只有二个零点的函数 |
函数f(x)=21-|x|的图象是( )
A、 |
B、 |
C、 |
D、 |
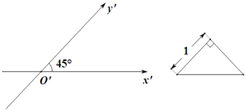 已知一个三棱锥的高为3,其底面用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如右图所示),则此三棱锥的体积为( )
已知一个三棱锥的高为3,其底面用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如右图所示),则此三棱锥的体积为( )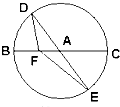 如图,BC是单位圆A的一条直径,F是线段AB上的点,且
如图,BC是单位圆A的一条直径,F是线段AB上的点,且