题目内容
已知函数f(x)=lg
,若f(a)=2,则f(-a)= .
| 1-x |
| 1+x |
考点:函数的值
专题:函数的性质及应用
分析:由已知得f(-x)=lg
=-f(x),由此能求出f(-a).
| 1-x |
| 1+x |
解答:
解:∵f(x)=lg
,
∴f(-x)=lg
=-f(x),
∵f(a)=2,
∴f(-a)=-f(a)=-2.
故答案为:-2.
| 1-x |
| 1+x |
∴f(-x)=lg
| 1-x |
| 1+x |
∵f(a)=2,
∴f(-a)=-f(a)=-2.
故答案为:-2.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意函数值的求法.

练习册系列答案
相关题目
点A、B、C、D在同一个球的球面上,且AB=CD=
,BC=2AC=2BD=2,则该球的表面积为( )
| 3 |
| A、16π | B、12π |
| C、8π | D、4π |
在△ABC中,已知角A,B,C所对的边分别为a,b,c,且a=3,c=8,B=60°,则△ABC的周长是( )
| A、17 | B、19 | C、16 | D、18 |
数列{an}的通项公式an=n2+2n,则数列{
}的前10项和为( )
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|
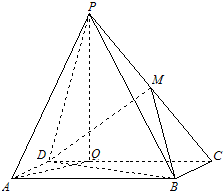 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,点P在底面的射影Q在CD上,且PQ=
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,点P在底面的射影Q在CD上,且PQ=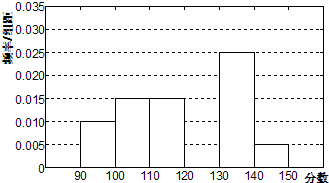 武汉外国语学校从参加高二年级期末考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图.观察图形的信息,回答如下问题:
武汉外国语学校从参加高二年级期末考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图.观察图形的信息,回答如下问题: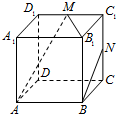 如图所示,在正方体ABCD A1B1C1D1中,M、N分别是棱C1D1,C1C的中点.给出以下四个结论:
如图所示,在正方体ABCD A1B1C1D1中,M、N分别是棱C1D1,C1C的中点.给出以下四个结论: