题目内容
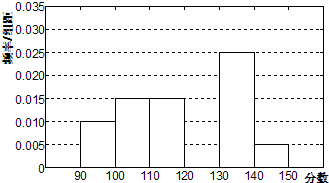 武汉外国语学校从参加高二年级期末考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图.观察图形的信息,回答如下问题:
武汉外国语学校从参加高二年级期末考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图.观察图形的信息,回答如下问题:(1)求分数在[120,130)内的频率,并补全这个频率分布直方图;
(2)用分层抽样的方法在分数段[110,130)的学生中抽取一个容量为6的样本,将样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
考点:古典概型及其概率计算公式,分层抽样方法,频率分布直方图
专题:概率与统计
分析:(1)由已知得分数在[120,130)内的频率为1-(0.1+0.15+0.15+0.25+0.05)=0.3,由此能补全直方图.
(2)用分层抽样的方法在分数段[110,130)的学生中抽取一个容量为6的样本,将样本看成一个总体,其中2人成绩在[110,120)之间,有4人成绩在[120,130)之间,由此能求出至多有1人在分数段[120,130)内的概率.
(2)用分层抽样的方法在分数段[110,130)的学生中抽取一个容量为6的样本,将样本看成一个总体,其中2人成绩在[110,120)之间,有4人成绩在[120,130)之间,由此能求出至多有1人在分数段[120,130)内的概率.
解答:
解:(1)由已知得分数在[120,130)内的频率为: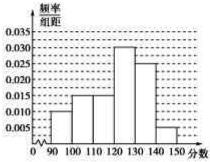
1-(0.1+0.15+0.15+0.25+0.05)=0.3,
=
=0.03,
补全后的直方图如下:
(2)用分层抽样的方法在分数段[110,130)的学生中抽取一个容量为6的样本,
将样本看成一个总体,其中2人成绩在[110,120)之间,有4人成绩在[120,130)之间,
∴至多有1人在分数段[120,130)内的概率:
p=1-
=
.

1-(0.1+0.15+0.15+0.25+0.05)=0.3,
| 频率 |
| 组距 |
| 0.3 |
| 10 |
补全后的直方图如下:
(2)用分层抽样的方法在分数段[110,130)的学生中抽取一个容量为6的样本,
将样本看成一个总体,其中2人成绩在[110,120)之间,有4人成绩在[120,130)之间,
∴至多有1人在分数段[120,130)内的概率:
p=1-
| ||
|
| 3 |
| 5 |
点评:本题考查频率直方图的应用,考查概率的求法,解题时要认真审题,注意等可能事件的概率计算公式的合理运用.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
为了得到函数y=sin(2x+2)的图象,只需把函数y=sin2x的图象上所有的点( )
| A、向左平行移动2个单位长度 |
| B、向右平行移动2个单位长度 |
| C、向左平行移动1个单位长度 |
| D、向右平行移动1个单位长度 |