Question

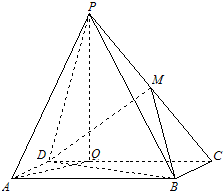如图，四棱锥P-ABCD中，底面ABCD是矩形，AB=4，AD=2，点P在底面的射影Q在CD上，且PQ=

15

，DQ=1．M为PC的中点．
（Ⅰ）证明：AD⊥平面PCD；
（Ⅱ）求直线AQ与平面MBD所成的角．

Answer 1

考点：直线与平面所成的角,直线与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（Ⅰ）首先根据线面垂直得到面面垂直，进一步得到线面垂直．
（Ⅱ）利用空间直角坐标系，和法向量求线面的夹角．

解答： 解（Ⅰ）证明  由题意可知，PQ⊥平面ABCD，
PQ?平面，
所以平面PCD⊥平面ABCD．
又因为AD⊥CD，
所以AD⊥平面PCD
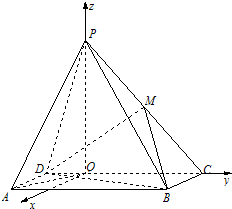
（Ⅱ）建立空间直角坐标系如图，由题设条件，相关各点的坐标分别是D（0，-1，0），M ( 0 ， 

3

2

 ， 

15

2

 )，A（2，-1，0），Q（0，0，0），B（2，3，0），
则

DB

= ( 2 ， 4， 0 )，

DM

=( 0 ， 

5

2

 ， 

15

2

 )．
设

n

=( x ， y ， z )是平面MBD的一个法向量，
由

n • DB =0 n • DM =0

得

2x+4y=0         5 2 y+ 15 2 z=0

．
取x=6，得

n

=( 6 ， -3 ， 

15

 )．
又

QA

= ( 2 ， -1 ， 0 )，所以cos＜

QA

，

n

＞=

QA • n

| QA |•| n |

=

15

5 • 60

=

3

2

．
从而直线AQ与平面MBD所成的角是60°．

点评：本题考查的知识要点：线面垂直的判定定理，面面垂直的性质定理，法向量的应用线面夹角的应用．