题目内容
某商品在近100天内,商品的单价f(t)(元)与时间t(天)的函数关系式如下:f(t)=
销售量g(t)与时间t(天)的函数关系式是g(t)=-
+
(0≤t≤100,t∈Z).求这种商品在这100天内哪一天的销售额最高?
|
| t |
| 3 |
| 112 |
| 3 |
考点:函数与方程的综合运用
专题:函数的性质及应用
分析:根据函数f(t)为分段函数,分段研究销售额函数的最值,即可求出分段函数的最值.
解答:
解:由题意,0≤t≤40,t∈Z时,销售额y=(
+22)(-
+
)=-
(t-12)2+
+12,
∴t=12时,ymax=
+12≈833;
当40<t≤100时,销售额y=(-
+52)(-
+
)=
(t2-216t)+
,
∴函数当40<t≤100时为减函数,
∴y<768.
综上,当0≤t≤100时,当且仅当t=12时,ymax≈833.
| t |
| 4 |
| t |
| 3 |
| 112 |
| 3 |
| 1 |
| 12 |
| 112×22 |
| 3 |
∴t=12时,ymax=
| 112×22 |
| 3 |
当40<t≤100时,销售额y=(-
| t |
| 2 |
| t |
| 3 |
| 112 |
| 3 |
| 1 |
| 6 |
| 52×112 |
| 3 |
∴函数当40<t≤100时为减函数,
∴y<768.
综上,当0≤t≤100时,当且仅当t=12时,ymax≈833.
点评:本题的考点是函数与方程的综合运用,考查函数模型的构建,考查分段函数的最值问题,解题时应搞清分段函数最值的求解方法.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知函数f(x)=|x2-6|,若a<b<0,且f(a)=f(b),则a2b的最小值是( )
| A、-16 | B、-12 |
| C、-10 | D、-8 |
若直线l:4x+3y+a=0和圆C:x2+y2+2x-4y+1=0有公共点,则实数a的取值范围是( )
| A、[-12,8] |
| B、[-8,12] |
| C、[-22,18] |
| D、[-18,22] |
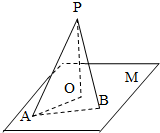 如图,直线PO⊥平面M,垂足为O,直线PA是平面M的一条斜线,斜足为A,其中∠APO=α,过点P的动直线PB交平面M于点B,∠APB=β,则下列说法正确的是
如图,直线PO⊥平面M,垂足为O,直线PA是平面M的一条斜线,斜足为A,其中∠APO=α,过点P的动直线PB交平面M于点B,∠APB=β,则下列说法正确的是