题目内容
已知A={1,2,4,5},a,b∈A则方程
+
=1表示焦点在y轴上的椭圆的概率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:椭圆的简单性质
专题:概率与统计
分析:首先求出构成椭圆的基本事件,进一步求出表示焦点在y轴上的椭圆的基本事件数,最后求出概率的值.
解答:
解:A={1,2,4,5},a,b∈A则方程
+
=1表示椭圆,
可分以下几种情况①当a=1时,b=2、4、5,
②a=2时,b=1、4、5,
③a=4时,b=1、2、5,
④a=5时,b=1、2、4,
所以表示椭圆的基本事件为:12;
焦点在y轴上的椭圆,
①当a=1时,b=2、4、5;
②a=2时,b=4、5;
③a=4时,b=5;
表示焦点在y轴上椭圆的基本事件为:6,
则表示焦点在y轴上的椭圆的概率为:P(A)=
;
故选:D.
| x2 |
| a2 |
| y2 |
| b2 |
可分以下几种情况①当a=1时,b=2、4、5,
②a=2时,b=1、4、5,
③a=4时,b=1、2、5,
④a=5时,b=1、2、4,
所以表示椭圆的基本事件为:12;
焦点在y轴上的椭圆,
①当a=1时,b=2、4、5;
②a=2时,b=4、5;
③a=4时,b=5;
表示焦点在y轴上椭圆的基本事件为:6,
则表示焦点在y轴上的椭圆的概率为:P(A)=
| 1 |
| 2 |
故选:D.
点评:本题考查的知识要点:古典概型问题,求古典概率的步骤.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤| π |
| 2 |
A、f(x)=2sin(2x-
| ||
B、f(x)=2sin(2x+
| ||
C、f(x)=2sin(2x+
| ||
D、f(x)=2sin(x+
|
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式与S=f(0)+f(1)+f(2)+…+f(2010)的值分别为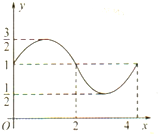 ( )
( )
 ( )
( )A、f(x)=
| ||||||
B、f(x)=sin
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
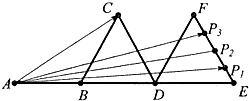 如图,△DBC,△DEF为边长为2的等边三角形,若AB=2,且P1,P2,P3是线段EF上的四等分点,则
如图,△DBC,△DEF为边长为2的等边三角形,若AB=2,且P1,P2,P3是线段EF上的四等分点,则 如图,设AD是△ABC的角平分线,AD交△ABC的外接圆与点E.求证:AB•AC=AD•AE.
如图,设AD是△ABC的角平分线,AD交△ABC的外接圆与点E.求证:AB•AC=AD•AE.