题目内容
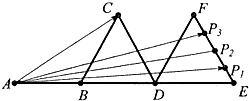如图，△DBC，△DEF为边长为2的等边三角形，若AB=2，且P1，P2，P3是线段EF上的四等分点，则| AC |
| AP1 |
| AC |
| AP2 |
| AC |
| AP3 |
| A、54 | ||
| B、18 | ||
C、18
| ||
| D、-18 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由图建立适当的平面直角坐标系，求出A，C，E，F的坐标，得到向量
，
，
的坐标，然后利用向量的加法运算把
•
+
•
+
•
转化为含
向量
，
，
的数量积，代入数量积的坐标运算求得
•
+
•
+
•
的值．
| AC |
| AE |
| AF |
| AC |
| AP1 |
| AC |
| AP2 |
| AC |
| AP3 |
向量
| AC |
| AE |
| AF |
| AC |
| AP1 |
| AC |
| AP2 |
| AC |
| AP3 |
解答：
解：建立如图所示的平面直角坐标系，
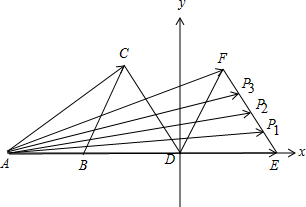
∵△DBC，△DEF为边长为2的等边三角形，且AB=2，
∴A（-4，0），C（-1，
），E（2，0），F（1，
），
=(3，
)，
=(6，0)，
=(5，
)．
又P1，P2，P3是线段EF上的四等分点，
则
•
+
•
+
•
=
(
+
+
)
=3
•
=
(
•
+
•
)
=
(3×6+
×0+3×5+
×
)=54．
故选：A．
∵△DBC，△DEF为边长为2的等边三角形，且AB=2，
∴A（-4，0），C（-1，
| 3 |
| 3 |
| AC |
| 3 |
| AE |
| AF |
| 3 |
又P1，P2，P3是线段EF上的四等分点，
则
| AC |
| AP1 |
| AC |
| AP2 |
| AC |
| AP3 |
| AC |
| AP1 |
| AP2 |
| AP3 |
=3
| AC |
| AP2 |
| 3 |
| 2 |
| AC |
| AE |
| AC |
| AF |
=
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
故选：A．
点评：本题考查了平面向量的数量积，考查了平面向量的坐标运算，关键是建立适当的平面直角坐标系，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
设集合A={x∈Z|x2＜4}，B={x|x＞-1}，则A∩B=（ ）
| A、{0，1} |
| B、{-1，0} |
| C、{-1，0，1} |
| D、{0，1，2} |
如图所示，点M在正六边形ABCDEF的边BC、CD、DE、EF上变动，若已知A={1，2，4，5}，a，b∈A则方程
+
=1表示焦点在y轴上的椭圆的概率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数在（1，+∞）上为增函数的是（ ）
| A、y=-|x-1| | ||
B、y=x+
| ||
C、y=
| ||
| D、y=x（2-x） |
如直线l1、l2的斜率是二次方程x2-4x+1=0的两根，那么l1与l2的夹角是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|