题目内容

等差数列{an}中，已知a2+a9=5，则3a5+a7的值为
 
．
考点：等差数列的性质
专题：等差数列与等比数列
分析：设等差数列{an}的公差为d，由已知条件可得2a1+9d=5，化简3a5+a7=2（2a1+9d），代入化简可得．
解答： 解：设等差数列{an}的公差为d，
则a2+a9=2a1+9d=5，
∴3a5+a7=3（a1+4d）+a1+6d
=4a1+18d=2（2a1+9d）=10
故答案为：10
点评：本题考查等差数列的性质，整体代换是解决问题的关键，属基础题．
练习册系列答案
相关题目
已知（1+2x）8展开式的二项式系数的最大值为a，系数的最大值为b，则
b
a
=（　　）
A、
128
5
B、
256
7
C、
512
5
D、
128
7
已知常数λ≥0，设各项均为正数的数列{an}的前n项和为Sn，满足：a1=1，Sn+1=
an+1
an
Sn+（λ•3n+1）an+1（n∈N*）．
（1）若λ=0，求数列{an}的通项公式；
（2）若an+1＜
1
2
an对一切n∈N*恒成立，求实数λ的取值范围．
在集合{1，2，3，4，5}中任取一个偶数a和一个奇数b构成以原点为起点的向量
a
=（a，b），从所得的以原点为起点的向量中任取两个向量为邻边作平行四边形，则平行四边形的面积等于2的概率为
 
．
已知△ABC的内角A，B，C所对的边分别为a，b，c，且a=2，b=3，cosB=
4
5
，则sinA的值为
 
．
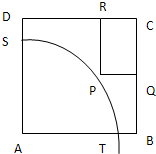如图：ABCD是一个边长为100m的正方形地皮，其中AST是一个半径为90m的扇形小山，其余部分都是平地，政府为方便附近住户，计划在平地上建立一个矩形停车场，使矩形的一个顶点P在弧
ST
上，相邻两边CQ、CR落在正方形的边BC、CD上，则矩形停车场PQCR的面积最小值为
 
m2．
已知cos2α-cos2β=m，那么sin（α+β）sin（α-β）=
 
．
已知抛物线C：y2=8x与点M（-2，2），过C的焦点，且斜率为k的直线与C交于A，B两点，若
MA
•
MB
=0，则k=
 
．
已知复数z满足z（1-i）=2i，其中i为虚数单位，则|z|=（　　）
A、1
B、
2
C、2
D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网