题目内容
已知cos2α-cos2β=m,那么sin(α+β)sin(α-β)= .
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:根据条件利用同角三角函数的基本关系、两角和差的正弦公式化简要求的式子,可得结果.
解答:
解:∵cos2α-cos2β=m,
∴sin(α+β)sin(α-β)=(sinαcosβ)2-(cosαsinβ)2
=sin2αcos2β-cos2α(1-cos2β)=sin2αcos2β-cos2α+cos2αcos2β
=(sin2αcos2β+cos2αcos2β)-cos2α=cos2β-cos2α=-m,
故答案为:-m.
∴sin(α+β)sin(α-β)=(sinαcosβ)2-(cosαsinβ)2
=sin2αcos2β-cos2α(1-cos2β)=sin2αcos2β-cos2α+cos2αcos2β
=(sin2αcos2β+cos2αcos2β)-cos2α=cos2β-cos2α=-m,
故答案为:-m.
点评:本题主要考查同角三角函数的基本关系、两角和差的正弦公式的应用,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
如图是一个组合几何体的三视图,则该几何体的体积是( )


A、
| ||||
B、
| ||||
| C、12+64π | ||||
| D、36+128π |
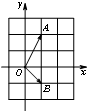 如图,在复平面内,若复数z1,z2对应的向量分别是
如图,在复平面内,若复数z1,z2对应的向量分别是| OA |
| OB |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知sinα-cosα=
,则cos2(
-α)=( )
| 1 |
| 3 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

