题目内容
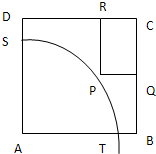 如图:ABCD是一个边长为100m的正方形地皮,其中AST是一个半径为90m的扇形小山,其余部分都是平地,政府为方便附近住户,计划在平地上建立一个矩形停车场,使矩形的一个顶点P在弧
如图:ABCD是一个边长为100m的正方形地皮,其中AST是一个半径为90m的扇形小山,其余部分都是平地,政府为方便附近住户,计划在平地上建立一个矩形停车场,使矩形的一个顶点P在弧 |
| ST |
考点:扇形面积公式
专题:应用题,三角函数的求值
分析:先建立直角坐标系,再设P(90cosx,90sinx),然后过P分别BC与CD的垂线,再求出PR,PQ的长度,然后建立面积模型,再按照函数模型求解最值.
解答:
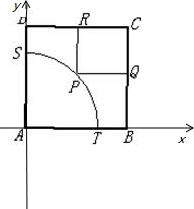 解:建立如图所示直角坐标系
解:建立如图所示直角坐标系
设P(90cosx,90sinx)
∴PR=100-90sinx,PQ=100-90cosx
∴sPQCR=(100-90sinx)(100-90cosx)
=10000-9000(sinx+cosx)+8100sinxcosx
令sinx+cosx=t∈[1,
]
∴sinxcosx=
∴sPQCR=4050t2-9000t+5950,
∴当t=
时,取得最小值950m2.
故答案为:950.
 解:建立如图所示直角坐标系
解:建立如图所示直角坐标系设P(90cosx,90sinx)
∴PR=100-90sinx,PQ=100-90cosx
∴sPQCR=(100-90sinx)(100-90cosx)
=10000-9000(sinx+cosx)+8100sinxcosx
令sinx+cosx=t∈[1,
| 2 |
∴sinxcosx=
| t2-1 |
| 2 |
∴sPQCR=4050t2-9000t+5950,
∴当t=
| 10 |
| 9 |
故答案为:950.
点评:本题主要考查函数模型的建立与应用,要注意先建系,再设点,表示相关的量,建立模型,最后解模型.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知数列{an}中,a1=25,4an+1=4an-7(n∈N*),若其前n项和为Sn,则Sn的最大值为( )
| A、15 | ||
| B、750 | ||
C、
| ||
D、
|
某学习小组男女生共8人,现从男生中选2人,女生中选1人,分别去做3中不同的工作,共有90种不同的选法,则男女生人数为( )
| A、2,6 | B、3,5 |
| C、5,3 | D、6,2 |
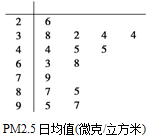 通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表:
通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表: