题目内容
已知常数λ≥0,设各项均为正数的数列{an}的前n项和为Sn,满足:a1=1,Sn+1=
Sn+(λ•3n+1)an+1(n∈N*).
(1)若λ=0,求数列{an}的通项公式;
(2)若an+1<
an对一切n∈N*恒成立,求实数λ的取值范围.
| an+1 |
| an |
(1)若λ=0,求数列{an}的通项公式;
(2)若an+1<
| 1 |
| 2 |
考点:数列的求和,数列递推式,数列与不等式的综合
专题:计算题,等差数列与等比数列
分析:(1)λ=0时,由已知Sn+1=
Sn+an+1写出Sn=
Sn作差求出数列{an}的通项公式;
(2)由已知求出
-
=λ3n+1,利用累加法求出
-1=λ(3+32+…+3n-1)+n-1,仿写作差求出λ表达式,构造数列bn=
求出其最大值,得到λ的范围.
| an+1 |
| an |
| an+1 |
| an |
(2)由已知求出
| Sn+1 |
| an+1 |
| Sn |
| an |
| Sn |
| an |
| 2n |
| 3n+3 |
解答:
解:(1)λ=0时,Sn+1=
Sn+an+1
∴Sn=
Sn
∵an>0,Sn>0
∴an+1=an,
∵a1=1,
∴an=1
(2)∵Sn+1=
Sn+(λ•3n+1)an+1(n∈N*).
∴
-
=λ3n+1,
则
-
=λ•3+1,
-
=λ•32+1,
∴
-
=λ3n-1+1.
相加得
-1=λ(3+32+…+3n-1)+n-1.
则Sn=(λ•
+n)•an,(n≥2)
上式对n=1也成立.
∴Sn=(λ•
+n)•an,
Sn+1=(λ•
+n+1)•an+1,(n≥2)
相减得an+1=(λ•
+n+1)•an+1-(λ•
+n)•an
即(λ•
+n)•an+1=(λ•
+n)•an
∵λ≥0,
∴(λ•
+n)>0,λ•
+n>0
∵an+1<
an对一切n∈N*恒成立,
∴(λ•
+n)<
(λ•
+n)对一切n∈N*恒成立,
即λ>
对一切n∈N*恒成立,
记bn=
则bn-bn+1=
-
=
当n=1时,bn-bn+1=0
当n≥2时bn-bn+1>0
∴当n=1时,bn=
有最大值
∴λ>
| an+1 |
| an |
∴Sn=
| an+1 |
| an |
∵an>0,Sn>0
∴an+1=an,
∵a1=1,
∴an=1
(2)∵Sn+1=
| an+1 |
| an |
∴
| Sn+1 |
| an+1 |
| Sn |
| an |
则
| S2 |
| a2 |
| S1 |
| a1 |
| S3 |
| a3 |
| S2 |
| a2 |
∴
| Sn |
| an |
| Sn-1 |
| an-1 |
相加得
| Sn |
| an |
则Sn=(λ•
| 3n-3 |
| 2 |
上式对n=1也成立.
∴Sn=(λ•
| 3n-3 |
| 2 |
Sn+1=(λ•
| 3n+1-3 |
| 2 |
相减得an+1=(λ•
| 3n+1-3 |
| 2 |
| 3n-3 |
| 2 |
即(λ•
| 3n+1-3 |
| 2 |
| 3n-3 |
| 2 |
∵λ≥0,
∴(λ•
| 3n-3 |
| 2 |
| 3n+1-3 |
| 2 |
∵an+1<
| 1 |
| 2 |
∴(λ•
| 3n-3 |
| 2 |
| 1 |
| 2 |
| 3n+1-3 |
| 2 |
即λ>
| 2n |
| 3n+3 |
记bn=
| 2n |
| 3n+3 |
则bn-bn+1=
| 2n |
| 3n+3 |
| 2n+2 |
| 3n+1+3 |
| (4n-2)3n-6 |
| (3n+3)(3n+1+3) |
当n=1时,bn-bn+1=0
当n≥2时bn-bn+1>0
∴当n=1时,bn=
| 2n |
| 3n+3 |
| 1 |
| 3 |
∴λ>
| 1 |
| 3 |
点评:本题考查数列求通项的方法;考查不等式恒成立转化为求最值,构造新数列的方法,属于一道综合题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
如图是一个组合几何体的三视图,则该几何体的体积是( )


A、
| ||||
B、
| ||||
| C、12+64π | ||||
| D、36+128π |
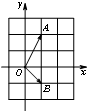 如图,在复平面内,若复数z1,z2对应的向量分别是
如图,在复平面内,若复数z1,z2对应的向量分别是| OA |
| OB |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |

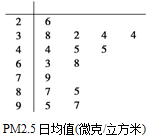 通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表:
通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表: