题目内容
在集合{1,2,3,4,5}中任取一个偶数a和一个奇数b构成以原点为起点的向量
=(a,b),从所得的以原点为起点的向量中任取两个向量为邻边作平行四边形,则平行四边形的面积等于2的概率为 .
| a |
考点:平面向量的综合题,几何概型
专题:平面向量及应用,概率与统计
分析:根据古典概型的概率公式,分别求出满足条件的a,b的取法,即可得到结论.
解答:
解:由题意知本题是一个古典概型,
试验发生包含的事件是取出数字,构成向量,
a的取法有2种,b的取法有3种,故向量
=(a,b)有6个,
分别为
1=(2,1),
2=(2,3),
3=(4,1),
4=(4,3),
=(2,5),
=(4,5),从中任取两个向量共C62=15种取法,
设两个非零向量
,
,它们的夹角为θ,则cosθ=
,
则sinθ=
=
,
∴对应平行四边形的面积S=2×
|
|•|
|sinθ=
,
则S=2,则(|
||
|)2-(
•
)2=4,
当
1=(2,1),
3=(4,1)时,满足条件,
当
1=(2,1),
4=(4,3)时,满足条件,
当
2=(2,3),
=(4,5),满足条件.
∴满足条件的事件列举法求出面积等于2的三角形的个数有3个,
∴根据古典概型概率公式得到P=
=
,
故答案为:
试验发生包含的事件是取出数字,构成向量,
a的取法有2种,b的取法有3种,故向量
| a |
分别为
| a |
| a |
| a |
| a |
| a5 |
| a6 |
设两个非零向量
| a |
| b |
| ||||
|
|
则sinθ=
| 1-cos2θ |
| ||||||||||
|
|
∴对应平行四边形的面积S=2×
| 1 |
| 2 |
| a |
| b |
(|
|
则S=2,则(|
| a |
| b |
| a |
| b |
当
| a |
| a |
当
| a |
| a |
当
| a |
| a6 |
∴满足条件的事件列举法求出面积等于2的三角形的个数有3个,
∴根据古典概型概率公式得到P=
| 3 |
| 15 |
| 1 |
| 5 |
故答案为:
| 1 |
| 5 |
点评:本题考查古典概型及其概率计算公式,考查平面向量的数量积的应用,综合性较强,难度较大.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
若直线y=2x+b被圆(x+1)2+y2=4所截得的弦最长,则b等于( )
| A、-1 | B、0 | C、1 | D、2 |
集合A={x|x2+x-6<0},B={y|y=lg(x2+1)},则A∩B等于( )
| A、(-3,2) |
| B、[0,3) |
| C、[0,+∞) |
| D、[0,2) |
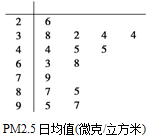 通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表:
通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表: