题目内容
已知有相同焦点F1、F2的椭圆
+y2=1(m>1)和双曲线
-y2=1(n>0),点P是它们的一个交点,则三角形F1PF2面积的大小是 .
| x2 |
| m |
| x2 |
| n |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用双曲线和椭圆的定义、余弦定理和三角形的面积计算公式,即可得出三角形的面积.
解答:
解:如图所示,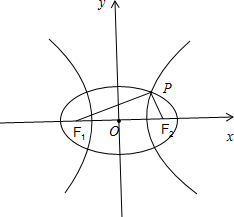 不妨设两曲线的交点P位于双曲线的右支上,设|PF1|=s,|PF2|=t.
不妨设两曲线的交点P位于双曲线的右支上,设|PF1|=s,|PF2|=t.
由双曲线和椭圆的定义可得
,
解得s2+t2=2m+2n,st=m-n.
在△PF1F2中,cos∠F1PF2=
=
∵m-1=n+1,
∴m-n=2,
∴cos∠F1PF2=0,∴∠F1PF2=90°.
∴△F1PF2面积为
st=1.
故答案为:1.
 不妨设两曲线的交点P位于双曲线的右支上,设|PF1|=s,|PF2|=t.
不妨设两曲线的交点P位于双曲线的右支上,设|PF1|=s,|PF2|=t.由双曲线和椭圆的定义可得
|
解得s2+t2=2m+2n,st=m-n.
在△PF1F2中,cos∠F1PF2=
| s2+t2-4c2 |
| 2st |
| 2m+2n-4(m-1) |
| 2m-2n |
∵m-1=n+1,
∴m-n=2,
∴cos∠F1PF2=0,∴∠F1PF2=90°.
∴△F1PF2面积为
| 1 |
| 2 |
故答案为:1.
点评:本题考查椭圆与双曲线方程及其几何性质及代数运算能力.熟练掌握双曲线和椭圆的定义、余弦定理和三角形的面积计算公式是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
给出下列命题:
①y=1是幂函数;
②函数f(x)=2x-log2x的零点有1个;
③
(x-2)≥0的解集为[2,+∞);
④“x<1”是“x<2”的充分不必要条件;
⑤函数y=x3在点O(0,0)处切线是x轴;
其中真命题的序号是( )
①y=1是幂函数;
②函数f(x)=2x-log2x的零点有1个;
③
| x-1 |
④“x<1”是“x<2”的充分不必要条件;
⑤函数y=x3在点O(0,0)处切线是x轴;
其中真命题的序号是( )
| A、①④ | B、④⑤ | C、③⑤ | D、②③ |
下列函数中是偶函数且在(0,+∞)上单调递增的是( )
| A、y=2-x |
| B、y=lnx |
| C、y=x-2 |
| D、y=|x|-1 |
函数y=
的图象大致是( )
| x3 |
| 3x-1 |
A、 |
B、 |
C、 |
D、 |
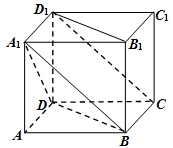 如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°
如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°