题目内容
已知集合{(x,y)|
}表示的平面区域为Ω,若在区域Ω内任取一点P(x,y),若u=
,则u的取值范围是 .
|
| 2x+y+3 |
| x+1 |
考点:简单线性规划
专题:计算题,作图题,不等式的解法及应用
分析:作出其平面区域,化简u=
=2+
,
可看成点P(x,y)与点A(-1,-1)构成的直线的斜率,从而求u的取值范围.
| 2x+y+3 |
| x+1 |
| y+1 |
| x+1 |
| y+1 |
| x+1 |
解答:
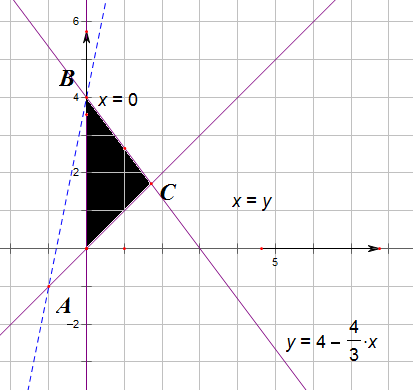 解:作出其平面区域如右图:
解:作出其平面区域如右图:
u=
=2+
,
可看成点P(x,y)与点A(-1,-1)构成的直线的斜率,
∵kAC=1,kAB=
=5,
∴1≤
≤5,
∴3≤2+
≤7,
故答案为[3,7].
 解:作出其平面区域如右图:
解:作出其平面区域如右图:u=
| 2x+y+3 |
| x+1 |
| y+1 |
| x+1 |
| y+1 |
| x+1 |
∵kAC=1,kAB=
| 4+1 |
| 0+1 |
∴1≤
| y+1 |
| x+1 |
∴3≤2+
| y+1 |
| x+1 |
故答案为[3,7].
点评:本题考查了简单线性规划,对于u=
=2+
的化简非常重要,属于基础题.
| 2x+y+3 |
| x+1 |
| y+1 |
| x+1 |

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知集合M={x||x|≥x2},N={x|y=2x-1,x∈R},则M∩N=( )
| A、(0,1] |
| B、(0,1) |
| C、[0,1) |
| D、[0,1] |
一个骰子由1-6六个数字组成,请你根据图中的三种状态所显示的数字,推出“?”处的数字式( )

| A、6 | B、3 | C、1 | D、2 |
若tan(
-α)=3,则tan2α=( )
| π |
| 4 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|