题目内容
给出下列命题:
①y=1是幂函数;
②函数f(x)=2x-log2x的零点有1个;
③
(x-2)≥0的解集为[2,+∞);
④“x<1”是“x<2”的充分不必要条件;
⑤函数y=x3在点O(0,0)处切线是x轴;
其中真命题的序号是( )
①y=1是幂函数;
②函数f(x)=2x-log2x的零点有1个;
③
| x-1 |
④“x<1”是“x<2”的充分不必要条件;
⑤函数y=x3在点O(0,0)处切线是x轴;
其中真命题的序号是( )
| A、①④ | B、④⑤ | C、③⑤ | D、②③ |
考点:命题的真假判断与应用
专题:简易逻辑
分析:对于①,根据幂函数的定义判断;
对于②:结合图象进行判断;
对于③:将问题转化为不等式组求解;
对于④:左右互相推导,然后下结论;
对于⑤:由题意(0,0)是切点,然后该处的导数值为切线斜率,据此写出切线方程.
对于②:结合图象进行判断;
对于③:将问题转化为不等式组求解;
对于④:左右互相推导,然后下结论;
对于⑤:由题意(0,0)是切点,然后该处的导数值为切线斜率,据此写出切线方程.
解答:
解:对于①:因为y=1(x∈R)不等同于y=x0(x≠0)故该函数不幂函数,故①假命题;
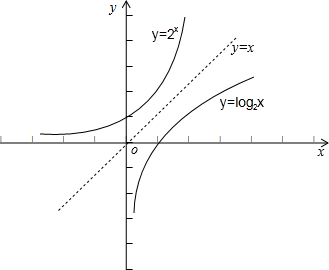
对于②:做出y=2x和y=log2x图象可知,两函数图象没有交点,故②为假;
对于③:由题意得:
或 x-1=0,解得x=1或x≥2,故③为假命题;
对于④:x<1⇒x<2成立,但x<2推不出x<1,故④真命题;
对于⑤:显然(0,0)是切点,且y′=3x2.此时斜率为k=0,所以切线方程是y=0,即为x轴,故⑤正确.
故选B.
对于②:做出y=2x和y=log2x图象可知,两函数图象没有交点,故②为假;

对于③:由题意得:
|
对于④:x<1⇒x<2成立,但x<2推不出x<1,故④真命题;
对于⑤:显然(0,0)是切点,且y′=3x2.此时斜率为k=0,所以切线方程是y=0,即为x轴,故⑤正确.
故选B.
点评:本题考查的知识点较多,要仔细辨析才能准确答题,要注意③⑤两个命题的辨析极为关键.

练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为斜边AB的中点,则
•
=( )
| AB |
| CD |
| A、1 | B、-1 | C、2 | D、-2 |