题目内容
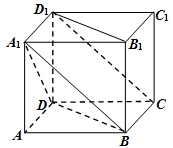 如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°
如图,在底面为平行四边形的四棱柱ABCD-A1B1C1D1中,D1D⊥底面ABCD,AD=1,CD=2,∠DCB=60°(1)求证:平面A1BCD1⊥平面BDD1B1
(2)若D1D=BD,求点D到平面A1BCD1.
考点:平面与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)首先利用勾股定理和余弦定理求出相关的线线垂直,进一步利用线面的垂直的判定和性质
转换为面面垂直的判定,从而证明结论.
(1)利用(1)的结论,进一步利用等面积法求的结果.
转换为面面垂直的判定,从而证明结论.
(1)利用(1)的结论,进一步利用等面积法求的结果.
解答:
证明:(1)在底面为平行四边形的四棱柱ABCD-A1B1C1D1中
D1D⊥底面ABCD,DD1⊥A1D1
AD=1,CD=2,∠DCB=60°利用余弦定理得:BD=
△BDC为直角三角形
BD⊥BC
AD⊥BD
∴A1D1⊥B1D1
所以A1D1⊥平面BDD1B1 A1D1?平面A1BCD1
所以:平面A1BCD1⊥平面BDD1B1
(2)解:连BD1,作DM⊥BD1
由(1)知
平面A1BCD1平面BDD1B1∵平面A1BCD1∩平面BDD1B1=BD1∴DM⊥平面A1BCD1
由已知BD=
∴DD1=
∵D1D⊥底面ABCD
∴DD1⊥BD∴BD1=
∴
×
×
=
×DM×
∴DM=
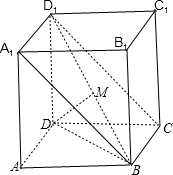
D1D⊥底面ABCD,DD1⊥A1D1
AD=1,CD=2,∠DCB=60°利用余弦定理得:BD=
| 3 |
△BDC为直角三角形
BD⊥BC
AD⊥BD
∴A1D1⊥B1D1
所以A1D1⊥平面BDD1B1 A1D1?平面A1BCD1
所以:平面A1BCD1⊥平面BDD1B1
(2)解:连BD1,作DM⊥BD1
由(1)知
平面A1BCD1平面BDD1B1∵平面A1BCD1∩平面BDD1B1=BD1∴DM⊥平面A1BCD1
由已知BD=
| 3 |
∴DD1=
| 3 |
∵D1D⊥底面ABCD
∴DD1⊥BD∴BD1=
| 6 |
∴
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 6 |
| ||
| 2 |

点评:本题考查的知识点:勾股定理得逆定理,余弦定理,线面垂直的性质与判定,面面垂直的判定以及等面积法的应用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
在Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为斜边AB的中点,则
•
=( )
| AB |
| CD |
| A、1 | B、-1 | C、2 | D、-2 |