题目内容
给出下列说法:
①不等于0的所有偶数可以组成一个集合;
②高一(1)班的所有高个子同学可以组成一个集合;
③{1,2,3,4}与{4,2,3,1}是不同的集合;
④实数中不是有理数的所有数能构成一个集合.
其中正确的个数是( )
①不等于0的所有偶数可以组成一个集合;
②高一(1)班的所有高个子同学可以组成一个集合;
③{1,2,3,4}与{4,2,3,1}是不同的集合;
④实数中不是有理数的所有数能构成一个集合.
其中正确的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①根据集合元素的特性“确定性”进行判断;
②“高个子”不明确,故不能构成集合;
③根据两个集合中的元素完全相同,则集合相等进行判断;
④显然判定一个对象是否属于该集合的条件明确,故④是真命题.
②“高个子”不明确,故不能构成集合;
③根据两个集合中的元素完全相同,则集合相等进行判断;
④显然判定一个对象是否属于该集合的条件明确,故④是真命题.
解答:
解:对于①④:由集合元素的特性“确定性”可知,题目所给的限制条件能够明确的判断一个对象是否为该集合的元素,故①④皆为真命题;
对于②:高个子不明确,不能说明怎样才算高个子,也就不能判断一位同学是否为该集合的元素,故③为假命题;
对于③:两集合相等只需元素完全相同即可,不需要顺序也相同,故③为假命题.
故选C.
对于②:高个子不明确,不能说明怎样才算高个子,也就不能判断一位同学是否为该集合的元素,故③为假命题;
对于③:两集合相等只需元素完全相同即可,不需要顺序也相同,故③为假命题.
故选C.
点评:本题考查了集合的定义、集合中元素的特性等知识,属基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知函数f(x)=
,若f(2-a2)<f(a),则实数a的取值范围是( )
|
| A、(-∞,-1)∪(2,+∞) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-∞,-2)∪(1,+∞) |
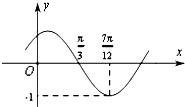 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<| π |
| 2 |
| π |
| 3 |
| A、f(x)=sin2x | ||
| B、f(x)=-sin2x | ||
C、f(x)=sin(2x-
| ||
D、f(x)=sin(2x+
|
函数f(x)=
(x∈R)的值域是( )
| x |
| x2+1 |
A、[-
| ||||
B、[0,
| ||||
C、(-
| ||||
D、[-
|