题目内容
设f(x)=|logmx|,其中m>0,m≠1,已知0<a<b,且满足f(a)=f(b)
(1)求证:a•b=1;
(2)比较
与1的大小;
(3)试问当m>1时,关于b的方程f(b)=2f(
)是否在(3,4)内有解?
(1)求证:a•b=1;
(2)比较
| a+b |
| 2 |
(3)试问当m>1时,关于b的方程f(b)=2f(
| a+b |
| 2 |
考点:函数与方程的综合运用,函数零点的判定定理,函数的零点与方程根的关系,不等式比较大小
专题:函数的性质及应用
分析:(1)利用m与1和0的大小,画出函数的图象然后证明a•b=1;
(2)利用(1)ab=1,化简
,构造函数φ(b)=
+b,(b>0,b≠1)利用函数的单调性求出函数的最小值然后与1比较大小;
(3)试问当m>1时,关于b的方程f(b)=2f(
),利用(2)函数的单调性以及函数的零点判定定理判断函数在(3,4)内有解的问题.
(2)利用(1)ab=1,化简
| a+b |
| 2 |
| 1 |
| b |
(3)试问当m>1时,关于b的方程f(b)=2f(
| a+b |
| 2 |
解答:
 解:(1)当m>1时,结合函数图象,由f(a)=f(b)可判断a∈(0,1),b∈(1,+∞),
解:(1)当m>1时,结合函数图象,由f(a)=f(b)可判断a∈(0,1),b∈(1,+∞),
从而-logma=logmb,从而logmab=0,故ab=1.
0<m<1时,同理有ab=1.(没讨论扣1分) …(4分)
(2)由(1)知
=
,
令φ(b)=
+b,(b>0,b≠1)
在(1,+∞)上任取b1,b2且1<b1<b2,
∵φ(b1)-φ(b2)=
+b1-(
+b2)
=(
-
)+(b1-b2)=
+(b1-b2)
=
<0,
∴φ(b1)<φ(b2),∴φ(b)在(1,+∞)上为增函数,
∴φ(b)>φ(1)=2.所以
>1.…(9分)
(3)由前知m>1时b>1,
>1,.∵f(b)=2f(
),
∴logmb=2logm
=logm2,
∴b=(
)2,
得4b=a2+b2+2ab,(ab=1)
+b2+2-4b=0.
令h(b)=
+b2+2-4b,
因为h(3)<0,h(4)>0,
根据函数零点存在性定理可知,
函数h(b)在(3,4)内一定存在零点,
即关于b的方程f(b)=2f(
)在(3,4)内有解.…(14分)
 解:(1)当m>1时,结合函数图象,由f(a)=f(b)可判断a∈(0,1),b∈(1,+∞),
解:(1)当m>1时,结合函数图象,由f(a)=f(b)可判断a∈(0,1),b∈(1,+∞),从而-logma=logmb,从而logmab=0,故ab=1.
0<m<1时,同理有ab=1.(没讨论扣1分) …(4分)
(2)由(1)知
| a+b |
| 2 |
| ||
| 2 |
令φ(b)=
| 1 |
| b |
在(1,+∞)上任取b1,b2且1<b1<b2,
∵φ(b1)-φ(b2)=
| 1 |
| b1 |
| 1 |
| b2 |
=(
| 1 |
| b1 |
| 1 |
| b2 |
| b2-b1 |
| b1b2 |
=
| (b1-b2)(b1b2-1) |
| b1b2 |
∴φ(b1)<φ(b2),∴φ(b)在(1,+∞)上为增函数,
∴φ(b)>φ(1)=2.所以
| a+b |
| 2 |
(3)由前知m>1时b>1,
| a+b |
| 2 |
| a+b |
| 2 |
∴logmb=2logm
| a+b |
| 2 |
∴b=(
| a+b |
| 2 |
得4b=a2+b2+2ab,(ab=1)
| 1 |
| b2 |
令h(b)=
| 1 |
| b2 |
因为h(3)<0,h(4)>0,
根据函数零点存在性定理可知,
函数h(b)在(3,4)内一定存在零点,
即关于b的方程f(b)=2f(
| a+b |
| 2 |
点评:本题考查函数的综合应用,构造法以及函数的单调性以及最值的求法,函数的零点的判定定理的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
已知△ABC的内角A,B,C所对应的边分别为a,b,c,若cosC>
,则△ABC的形状是( )
| b |
| a |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、钝角三角形 |
公比为q的等比数列{an}的各项为正数,且a2a12=16,logqa10=7,则公比q=( )
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
若集合A={x|x2-1≤0},B={x|
≤0},则A∩B=( )
| x-2 |
| x |
| A、{x|-1≤x<0} |
| B、{x|0<x≤1} |
| C、{x|0≤x≤2} |
| D、{x|0≤x≤1} |
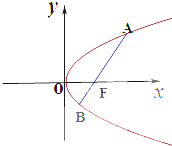 如图,给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点
如图,给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点