题目内容
已知:等差数列{an}中,a3+a4=15,a2a5=54,公差d<0.
(1)求数列{an}的通项公式an;
(2)求
的最大值及相应的n的值.
(1)求数列{an}的通项公式an;
(2)求
| Sn-an |
| n |
考点:等差数列的性质
专题:导数的综合应用,等差数列与等比数列
分析:(1)利用等差数列的性质结合已知列式求得首项和公差,代入等差数列的通项公式得答案;
(2)求出等差数列的前n项和,代入
整理,然后利用导数求最值,且求出n的值.
(2)求出等差数列的前n项和,代入
| Sn-an |
| n |
解答:
解:(1)∵数列{an}为等差数列,
∴a2+a5=a3+a4=15,
∴
,解得
或
,
∵d<0,
∴a2=9,a5=6,
则a1=10,d=-1.
∴an=11-n;
(2)∵a1=10,an=11-n,
∴Sn=-
n2+
n,
=
=-
(n+
)+
.
令f(x)=x+
,f′(x)=1-
=0,
知f(x)在(0,
)上单减,在(
,+∞)上单增,
又4<
<5,
而f(4)=9
>f(5)=9
.
∴当n=5时,
取最大值为-
×
+
=
.
∴a2+a5=a3+a4=15,
∴
|
|
|
∵d<0,
∴a2=9,a5=6,
则a1=10,d=-1.
∴an=11-n;
(2)∵a1=10,an=11-n,
∴Sn=-
| 1 |
| 2 |
| 21 |
| 2 |
| Sn-an |
| n |
-
| ||||
| n |
| 1 |
| 2 |
| 22 |
| n |
| 23 |
| 2 |
令f(x)=x+
| 22 |
| x |
| 22 |
| x2 |
知f(x)在(0,
| 22 |
| 22 |
又4<
| 22 |
而f(4)=9
| 1 |
| 2 |
| 2 |
| 5 |
∴当n=5时,
| Sn-an |
| n |
| 1 |
| 2 |
| 47 |
| 5 |
| 23 |
| 2 |
| 34 |
| 5 |
点评:本题考查了等差数列的性质,考查了等差数列的前n项和,训练了利用导数研究函数的单调性,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若A={x|log2(x-4)<1},B={y|y=3x+2,-4≤x≤3},则A∩B=( )
| A、[-10,6) |
| B、(4,6) |
| C、(6,11] |
| D、(0,11] |
下列函数中,既是偶函数又在区间(-∞,0)上单调递增的是( )
| A、f(x)=2-x | ||
| B、f(x)=x2+1 | ||
C、f(x)=
| ||
| D、f(x)=x3 |
已知sinθ+cosθ=
,θ∈(0,π),则tanθ=( )
| 1 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
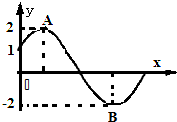 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤