题目内容
若0<x<1,则函数f(x)=
+
的最小值是 .
| 2 |
| x |
| 8 |
| 1-x |
考点:基本不等式
专题:导数的综合应用
分析:利用导数研究函数的单调性极值与最值即可得出.
解答:
解:∵0<x<1,函数f′(x)=-
+
=
,
∴当f′(x)>0时,解得
<x<1,此时函数f(x)单调递增;当f′(x)<0时,解得0<x<
,此时函数f(x)单调递减.
令f′(x)=0,解得x=
.
∴当x=
时,函数f(x)取得极小值即最小值18.
故答案为:18.
| 2 |
| x2 |
| 8 |
| (1-x)2 |
| 2(3x-1)(x+1) |
| (x-x2)2 |
∴当f′(x)>0时,解得
| 1 |
| 3 |
| 1 |
| 3 |
令f′(x)=0,解得x=
| 1 |
| 3 |
∴当x=
| 1 |
| 3 |
故答案为:18.
点评:本题考查了利用导数研究函数的单调性极值与最值,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
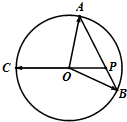 如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若
如图,A,B,C是圆O上的三点,线段AB交CO延长线于点P,若| OC |
| OA |
| OB |
| A、(-1,0) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、(-1,0)∪(0,1) |
给出下列函数(1)y=x2+|x|+2,x≤0(2)y=t2-t+2,t≤0(3)y=x2-|x|+2,x≥0(4)y=(
)4+
+2,其中与函数y=x2-x+2,x≤0相等的有( )
| x |
| x2 |
| A、(1) |
| B、(1)(2) |
| C、(1)(2)(4) |
| D、(1)(3)(4) |
若A={x|log2(x-4)<1},B={y|y=3x+2,-4≤x≤3},则A∩B=( )
| A、[-10,6) |
| B、(4,6) |
| C、(6,11] |
| D、(0,11] |
已知x4=81,那么x等于( )
| A、3 | B、-3 |
| C、-3或3 | D、不存在 |
若n<m<0,则
-
等于( )
| m2+2mn+n2 |
| m2-2mn+n2 |
| A、2m | B、2n |
| C、-2m | D、-2n |