题目内容
已知△ABC的内角A,B,C所对应的边分别为a,b,c,若cosC>
,则△ABC的形状是( )
| b |
| a |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、钝角三角形 |
考点:三角形的形状判断
专题:解三角形
分析:利用正弦定理可得sinAcosC>sinB,再利用两角和的正弦计算可得cosA<0,从而可得答案.
解答:
解:△ABC中,∵cosC>
,
∴由正弦定理得:cosC>
,又sinA>0,
∴sinAcosC>sinB=sin(A+C)=sinAcosC+cosAsinC,
∴cosAsinC<0,又sinC>0,
∴cosA<0,A为钝角,
故选:D.
| b |
| a |
∴由正弦定理得:cosC>
| sinB |
| sinA |
∴sinAcosC>sinB=sin(A+C)=sinAcosC+cosAsinC,
∴cosAsinC<0,又sinC>0,
∴cosA<0,A为钝角,
故选:D.
点评:本题考查三角形的形状的判断,考查正弦定理与两角和的正弦的应用,属于中档题.

练习册系列答案
相关题目
已知x4=81,那么x等于( )
| A、3 | B、-3 |
| C、-3或3 | D、不存在 |
已知某几何体的三视图如图所示,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )
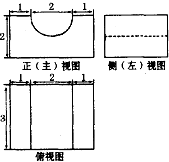

A、24-
| ||
B、24-
| ||
| C、24-π | ||
D、24-
|
已知定义在R上的奇函数f(x),且为减函数,又知f(1-a)+f(1-a2)<0,则a的取值范围为( )
| A、(-2,1) |
| B、(-∞,-2)∪(1,+∞) |
| C、(0,1) |
| D、(0,2) |
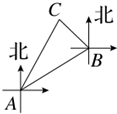 如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A处出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.
如图,某海上缉私小分队驾驶缉私艇以40km/h的速度由A处出发,沿北偏东60°方向进行海面巡逻,当航行半小时到达B处时,发现北偏西45°方向有一艘船C,若船C位于A的北偏东30°方向上,则缉私艇所在的B处与船C的距离是( )km.A、5(
| ||||
B、5(
| ||||
C、10(
| ||||
D、10(
|
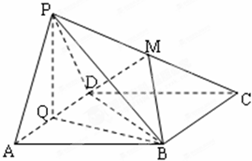 如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图:AD=2,AB=4的长方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.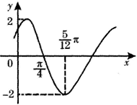 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<