题目内容

若集合A={x|x2-1≤0}，B={x|
x-2
x
≤0}，则A∩B=（　　）
A、{x|-1≤x＜0}
B、{x|0＜x≤1}
C、{x|0≤x≤2}
D、{x|0≤x≤1}
考点：其他不等式的解法,交集及其运算
专题：不等式的解法及应用
分析：利用分式不等式的解法求出集合B，二次不等式的解法求出A，然后求解交集．
解答： 解：集合A={x|x2-1≤0}={x|-≤x≤1}，
B={x|
x-2
x
≤0}={x|0＜x≤2}，
则A∩B={x|0＜x≤1}．
故选：B．
点评：本题考查不等式的解法，交集的求法，基本知识的考查．
练习册系列答案
相关题目
设f（x）=|logmx|，其中m＞0，m≠1，已知0＜a＜b，且满足f（a）=f（b）
（1）求证：a•b=1；
（2）比较
a+b
2
与1的大小；
（3）试问当m＞1时，关于b的方程f（b）=2f（
a+b
2
）是否在（3，4）内有解？
若n＜m＜0，则
m2+2mn+n2
-
m2-2mn+n2
等于（　　）
A、2mB、2n
C、-2mD、-2n
函数y=ax在[0，1]上的最大值与最小值和为3，则函数y=
a
2
x2+bx+3在[0，+∞）上是单调函数，则有（　　）
A、b＞0B、b＜0
C、b≥0D、b≤0
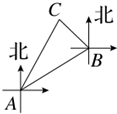如图，某海上缉私小分队驾驶缉私艇以40km/h的速度由A处出发，沿北偏东60°方向进行海面巡逻，当航行半小时到达B处时，发现北偏西45°方向有一艘船C，若船C位于A的北偏东30°方向上，则缉私艇所在的B处与船C的距离是（　　）km．
A、5（
6
+
2
）
B、5（
6
-
2
）
C、10（
6
-
2
）
D、10（
6
+
2
）
已知sinθ+cosθ=
1
5
，θ∈（0，π），则tanθ=（　　）
A、-
4
3
B、
4
3
C、-
3
4
D、
3
4
设集合M={x|y=
3-2x
}，N={y|y=3-2x}，则M∩N=
 
．
若log72=a，log73=b，则log76=（　　）
A、a+b
B、ab
C、
a
b
D、
b
a
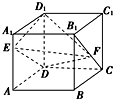如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别为线段AA1，B1C上的点，则三棱锥D1-EDF的体积为（　　）
A、
1
8
B、
1
6
C、
1
3
D、
1
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网