题目内容
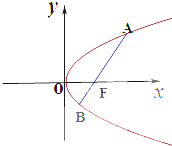 如图,给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点
如图,给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点(1)设l的斜率为1,求以AB为直径的圆的方程;
(2)若
| FA |
| BF |
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设A,B两点坐标,联立中心与抛物线组成方程组,求得AB的中点坐标,求出AB的长,然后求以AB为直径的圆的方程;
(2)设出A、B坐标,利用|FA|=2|BF|,转化为向量共线关系,以及A、B在直线和抛物线上,求出A、B坐标然后求直线l的方程.
(2)设出A、B坐标,利用|FA|=2|BF|,转化为向量共线关系,以及A、B在直线和抛物线上,求出A、B坐标然后求直线l的方程.
解答:
解:(1)由题意,得F(1,0),直线l的方程为y=x-1.
代入抛物线方程,得x2-6x+1=0,
设A,B两点坐标为A(x1,y1),B(x2,y2),AB中点M的坐标为M(x0,y0),
因为△=62-4=32>0,所以x1+x2=6,x1x2=1,
所以圆心为M(3,2),
由抛物线定义,得|AB|=|AF|+|BF|=x1+x2+p=8(其中p=2).
所以以AB为直径的圆的方程为(x-3)2+(y-2)2=16;
(2)因为|FA|=2|BF|,三点A,F,B共线且点A,B在点F两侧,
所以设A,B两点坐标为A(x1,y1),B(x2,y2),则
=(x1-1,y1),
=(1-x2,-y2),
所以x1-1=2(1-x2),y1=-2y2…①
设直线AB的方程为y=k(x-1)或x=1(不符合题意,舍去).
代入抛物线方程,得ky2-4y-4k=0,
因为直线l与C相交于A,B两点,所以k≠0,
则△=16+16k2>0,y1+y2=
,y1y2=-4,…②
由①②,得方程组k=±2
,
故直线l的方程为y=±2
(x-1).
代入抛物线方程,得x2-6x+1=0,
设A,B两点坐标为A(x1,y1),B(x2,y2),AB中点M的坐标为M(x0,y0),
因为△=62-4=32>0,所以x1+x2=6,x1x2=1,
所以圆心为M(3,2),
由抛物线定义,得|AB|=|AF|+|BF|=x1+x2+p=8(其中p=2).
所以以AB为直径的圆的方程为(x-3)2+(y-2)2=16;
(2)因为|FA|=2|BF|,三点A,F,B共线且点A,B在点F两侧,
所以设A,B两点坐标为A(x1,y1),B(x2,y2),则
| FA |
| BF |
所以x1-1=2(1-x2),y1=-2y2…①
设直线AB的方程为y=k(x-1)或x=1(不符合题意,舍去).
代入抛物线方程,得ky2-4y-4k=0,
因为直线l与C相交于A,B两点,所以k≠0,
则△=16+16k2>0,y1+y2=
| 4 |
| k |
由①②,得方程组k=±2
| 2 |
故直线l的方程为y=±2
| 2 |
点评:本题考查圆的方程,直线和圆的方程的应用,考查转化思想,函数与方程的思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
给出下列函数(1)y=x2+|x|+2,x≤0(2)y=t2-t+2,t≤0(3)y=x2-|x|+2,x≥0(4)y=(
)4+
+2,其中与函数y=x2-x+2,x≤0相等的有( )
| x |
| x2 |
| A、(1) |
| B、(1)(2) |
| C、(1)(2)(4) |
| D、(1)(3)(4) |
已知x4=81,那么x等于( )
| A、3 | B、-3 |
| C、-3或3 | D、不存在 |
已知某几何体的三视图如图所示,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )
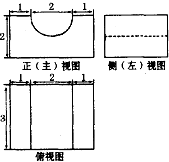

A、24-
| ||
B、24-
| ||
| C、24-π | ||
D、24-
|
已知定义在R上的奇函数f(x),且为减函数,又知f(1-a)+f(1-a2)<0,则a的取值范围为( )
| A、(-2,1) |
| B、(-∞,-2)∪(1,+∞) |
| C、(0,1) |
| D、(0,2) |
若n<m<0,则
-
等于( )
| m2+2mn+n2 |
| m2-2mn+n2 |
| A、2m | B、2n |
| C、-2m | D、-2n |