题目内容
若函数f(x)=2x2-lnx在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
| A、[1,3) | ||||
B、[1,
| ||||
C、(-
| ||||
D、[-
|
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:先确定函数的定义域然后求导数fˊ(x),在函数的定义域内解方程fˊ(x)=0,使方程的解在定义域内的一个子区间
(k-1,k+1)内,建立不等关系,解之即可
(k-1,k+1)内,建立不等关系,解之即可
解答:
解:因为f(x)定义域为(0,+∞),又f′(x)=4x-
,
由f'(x)=0,得x=
.
当x∈(0,
)时,f'(x)<0,当x∈(
,+∞)时,f'(x)>0
据题意,
,
解得1≤k<
,
故选:B.
| 1 |
| x |
由f'(x)=0,得x=
| 1 |
| 2 |
当x∈(0,
| 1 |
| 2 |
| 1 |
| 2 |
据题意,
|
解得1≤k<
| 3 |
| 2 |
故选:B.
点评:本题主要考查了对数函数的导数,以及利用导数研究函数的单调性等基础知识,考查计算能力,属于基础题.

练习册系列答案
相关题目
命题“?x∈[0,+∞),x2-x+1≥0”的否定是( )
| A、?x∈[0,+∞),x2-x+1<0 |
| B、?x∈(-∞,0),x2-x+1≥0 |
| C、?x0∈[0,+∞),x2-x+1<0 |
| D、?x0∈[0,+∞),x2-x+1≥0 |
双曲线
-
=1与椭圆
+
=1(a>0,m>b>0)的离心率互为倒数,则( )
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| m2 |
| y2 |
| b2 |
| A、a2+b2=m2 |
| B、a+b=m |
| C、a2=b2+m2 |
| D、a=b+m |
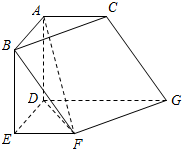 在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.AB=AC=FE=1,DG=2.
在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.AB=AC=FE=1,DG=2.