题目内容
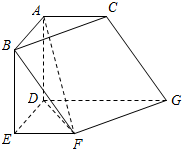 在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.AB=AC=FE=1,DG=2.
在如图所示的几何体中,四边形ABED是矩形,四边形ADGC是梯形,AD⊥平面DEFG,EF∥DG,∠EDG=120°.AB=AC=FE=1,DG=2.(Ⅰ)求证:AE∥平面BFGC;
(Ⅱ)求证:FG⊥平面ADF.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)连接CF,只要证明AE∥FC,利用线面平行的判定定理即可证明;
(Ⅱ)连接DF,AF,作DG的中点为H,连接EH,只要证明FG垂直DF,AD,利用线面垂直的判定定理.
(Ⅱ)连接DF,AF,作DG的中点为H,连接EH,只要证明FG垂直DF,AD,利用线面垂直的判定定理.
解答:
 证明:(Ⅰ)连接CF,
证明:(Ⅰ)连接CF,
∵AC∥DG,EF∥DG,
∴AC∥EF又AC=EF,
∴四边形AEFC是平行四边形,
∴AE∥FC,
又AE?平面BFGC,FC?平面BFGC,
∴AE∥平面BFGC;
(Ⅱ)连接DF,AF,作DG的中点为H,连接EH,
∵EF∥DH,EF=DH=ED=1,
∴四边形DEFH为菱形,
∵EF∥HG,EF=HG,
∴四边形DEFH为平行四边形,
∴FG∥EH,
∴FG⊥DF,
∵AD⊥平面DEFG,
∴AD⊥FG,
∵FG⊥DF,AD∩DF=D,
∴FG⊥面ADF.
 证明:(Ⅰ)连接CF,
证明:(Ⅰ)连接CF,∵AC∥DG,EF∥DG,
∴AC∥EF又AC=EF,
∴四边形AEFC是平行四边形,
∴AE∥FC,
又AE?平面BFGC,FC?平面BFGC,
∴AE∥平面BFGC;
(Ⅱ)连接DF,AF,作DG的中点为H,连接EH,

∵EF∥DH,EF=DH=ED=1,
∴四边形DEFH为菱形,
∵EF∥HG,EF=HG,
∴四边形DEFH为平行四边形,
∴FG∥EH,
∴FG⊥DF,
∵AD⊥平面DEFG,
∴AD⊥FG,
∵FG⊥DF,AD∩DF=D,
∴FG⊥面ADF.
点评:本题考查了线面平行的判定定理以及线面垂直的判定定理的运用;关键是将线面关系转化为线线关系进行证明.

练习册系列答案
相关题目
设函数f(x)的定义域为D,若任取x1∈D,存在唯一的x2∈D,满足
=C,则称C为函数y=f(x)在D上的均值,给出下列五个函数:①y=x;②y=x2;③y=4sinx;④y=lgx;⑤y=2x.则所有满足在其定义域上的均值为2的函数的序号为( )
| f(x1)+f(x2) |
| 2 |
| A、①③ | B、①④ |
| C、①④⑤ | D、②③④⑤ |
已知向量
=(1,1),b=(x2,x+2),若
,
共线,则实数x的值为( )
| a |
| a |
| b |
| A、-1 | B、2 |
| C、-1或2 | D、1或-2 |
若函数f(x)=2x2-lnx在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
| A、[1,3) | ||||
B、[1,
| ||||
C、(-
| ||||
D、[-
|
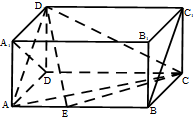 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动 某果林培育基地从其培育的一批幼苗中随机选取了100株,测量其高度(单位:厘米),并将这些数据绘制成频率分布直方图(如图).若要从高度在[120,130),[130,140),[140,150]三组内的幼苗中,用分层抽样的方法选取30株送给友好单位,则从高度在[140,150]内的幼苗中选取的株数应为( )
某果林培育基地从其培育的一批幼苗中随机选取了100株,测量其高度(单位:厘米),并将这些数据绘制成频率分布直方图(如图).若要从高度在[120,130),[130,140),[140,150]三组内的幼苗中,用分层抽样的方法选取30株送给友好单位,则从高度在[140,150]内的幼苗中选取的株数应为( )