题目内容
6.平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为150°,$\overrightarrow a=(2,0)$,$|{\overrightarrow b}|=2$则$|{\overrightarrow a+\sqrt{3}\overrightarrow b}|$=2.分析 利用两个向量的数量积的定义求得$\overrightarrow{a}•\overrightarrow{b}$ 的值,从而求得$|{\overrightarrow a+\sqrt{3}\overrightarrow b}|$=$\sqrt{{(\overrightarrow{a}+\sqrt{3}\overrightarrow{b})}^{2}}$ 的值.
解答 解:∵向量$\overrightarrow a$与$\overrightarrow b$的夹角为150°,$\overrightarrow a=(2,0)$,∴|$\overrightarrow{a}$|=2,
又$|{\overrightarrow b}|=2$,∴$\overrightarrow{a}•\overrightarrow{b}$=2•2•cos150°=-2$\sqrt{3}$,
则$|{\overrightarrow a+\sqrt{3}\overrightarrow b}|$=$\sqrt{{(\overrightarrow{a}+\sqrt{3}\overrightarrow{b})}^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}+2\sqrt{3}\overrightarrow{a}•\overrightarrow{b}+{3\overrightarrow{b}}^{2}}$=$\sqrt{4-12+3×4}$=2,
故答案为:2.
点评 本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题.

练习册系列答案
相关题目
16.平行于直线l:2x-y=0且与圆x2+y2=5相切的直线的方程是( )
| A. | 2x-y+=0或2x-y-=0 | B. | 2x+y+=0或2x+y-=0 | ||
| C. | 2x-y+5=0或2x-y-5=0 | D. | 2x+y+5=0或2x+y-5=0 |
1.若$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=\sqrt{2}$,($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=0,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | 30° | B. | 45° | C. | 135° | D. | 150° |
11.已知△ABC中,内角A、B、C所对的边分别为a、b、c,若a2=b2+c2-bc,a=3,则△ABC的面积的最大值为( )
| A. | $2\sqrt{3}$ | B. | 9 | C. | $\frac{{9\sqrt{3}}}{2}$ | D. | $\frac{{9\sqrt{3}}}{4}$ |
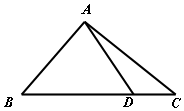 如图,已知D是△ABC边BC上一点.
如图,已知D是△ABC边BC上一点.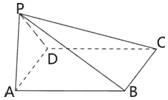 如图,平面PAD⊥平面ABCD,ABCD是边长为2的菱形,PA=PD,且∠APD=90°,∠DAB=60°.
如图,平面PAD⊥平面ABCD,ABCD是边长为2的菱形,PA=PD,且∠APD=90°,∠DAB=60°.