题目内容
14.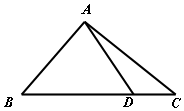 如图,已知D是△ABC边BC上一点.
如图,已知D是△ABC边BC上一点.(1)若B=45°,且AB=DC=7,求△ADC的面积;
(2)当∠BAC=90°时,若BD:DC:AC=2:1:$\sqrt{3}$,且AD=2$\sqrt{2}$,求DC的长.
分析 (1)过A点作AE⊥BC,交BC于点E,由已知可求AE,进而利用三角形面积公式即可计算得解.
(2)设CD=x,则BD=2x,AC=$\sqrt{3}$x,可求BC=3x,AB=$\sqrt{6}$x,进而利用余弦定理,三角函数的定义建立方程即可解得DC的值.
解答 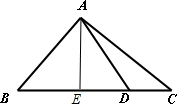 解:(1)过A点作AE⊥BC,交BC于点E,
解:(1)过A点作AE⊥BC,交BC于点E,
∵B=45°,且AB=DC=7,则AE=ABsinB=$\frac{7\sqrt{2}}{2}$,
可得:S△ADC=$\frac{1}{2}$DC•AE=$\frac{1}{2}×7×\frac{7\sqrt{2}}{2}$=$\frac{49\sqrt{2}}{4}$.
(2)设CD=x,则BD=2x,AC=$\sqrt{3}$x,
∴BC=CD+BD=3x,AB=$\sqrt{B{C}^{2}-A{C}^{2}}$=$\sqrt{6}$x,
∴cosC=$\frac{D{C}^{2}+A{C}^{2}-A{D}^{2}}{2AC•DC}$=$\frac{AC}{BC}$,可得:$\frac{{x}^{2}+3{x}^{2}-8}{2\sqrt{2}{x}^{2}}$=$\frac{\sqrt{3}x}{3x}$=$\frac{\sqrt{3}}{3}$,解得:x=2.
∴CD=2.
点评 本题主要考查了三角形的面积公式,余弦定理在解三角形中的应用,考查了转化思想和数形结合思想的应用,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
4.下列函数为偶函数的是( )
| A. | y=x-1 | B. | y=$\sqrt{x}$ | C. | y=x2 | D. | y=x3 |
5.抛物线C:y2=2px(p>0)的焦点与圆F:x2+y2-4x=0的圆心重合,点A,B,C在该抛物线上,且点F是△ABC的重心,则|FA|+|FB|+|FC|的值是( )
| A. | 6 | B. | 8 | C. | 9 | D. | 12 |
9.命题“?x∈R,f(x)>0”的否定为( )
| A. | ?x0∈R,f(x0)>0 | B. | ?x∈R,f(x)<0 | C. | ?x0∈R,f(x0)≤0 | D. | ?x∈R,f(x)≤0 |
3.已知关于x的不等式x2-4ax+3a2<0(a<0)的解集为(x1,x2),则${x_1}+{x_2}+\frac{a}{{{x_1}{x_2}}}$的最大值是( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $-\frac{{4\sqrt{3}}}{3}$ |