题目内容
16．平行于直线l：2x-y=0且与圆x2+y2=5相切的直线的方程是（ ）| A． | 2x-y+=0或2x-y-=0 | B． | 2x+y+=0或2x+y-=0 | ||
| C． | 2x-y+5=0或2x-y-5=0 | D． | 2x+y+5=0或2x+y-5=0 |
分析 先设出与2x-y+5=0平行的直线系方程2x-y+c=0，利用圆心到直线的距离求出参数c．
解答 解：设所求切线方程为2x-y+c=0，依题有$\frac{|0+0+c|}{\sqrt{4+1}}=\sqrt{5}$，解得c=±5，所以所求的直线方程为2x-y+5=0或2x-y-5=0．
故选C．
点评 本题考查直线方程，考查直线与圆的位置关系，属于中档题．
练习册系列答案
相关题目
4．下列函数为偶函数的是（ ）
| A． | y=x-1 | B． | y=$\sqrt{x}$ | C． | y=x2 | D． | y=x3 |
11．已知集合A={x|x2-x-2≤0}，B={x|log2x＞1}，则A∩（∁RB）=（ ）
| A． | （0，2] | B． | （0，2） | C． | [-1，2] | D． | （-1，2] |
1．
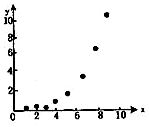如图所示的散点图，现选用两种回归模型，模型A：使用线性回归，计算相关指数$R_1^2$；模型B：用指数回归，计算出相关指数$R_2^2$，则一定有（ ）
如图所示的散点图，现选用两种回归模型，模型A：使用线性回归，计算相关指数$R_1^2$；模型B：用指数回归，计算出相关指数$R_2^2$，则一定有（ ）| A． | $R_1^2＞R_2^2$ | B． | $R_1^2＜R_2^2$ | C． | $R_1^2=R_2^2$ | D． | 无法确定 |
8．函数f（x）=48x-x3，x∈[-3，5]的最小值为（ ）
| A． | 128 | B． | -128 | C． | -117 | D． | 115 |