题目内容
11．已知△ABC中，内角A、B、C所对的边分别为a、b、c，若a2=b2+c2-bc，a=3，则△ABC的面积的最大值为（ ）| A． | $2\sqrt{3}$ | B． | 9 | C． | $\frac{{9\sqrt{3}}}{2}$ | D． | $\frac{{9\sqrt{3}}}{4}$ |
分析 由余弦定理可得：3=b2+c2-2bccosA=b2+c2-bc，从而解得bc≤3，利用三角形面积公式即可得解．
解答 解：∵a2=b2+c2-bc，
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{bc}{2bc}$=$\frac{1}{2}$，
∵A∈（0，π），
∴A=$\frac{π}{3}$，
又∵a=3，
∴由余弦定理可得：9=b2+c2-2bccosA=b2+c2-bc≥bc，解得：bc≤9，（当且仅当b=c时等号成立）．
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc≤$\frac{\sqrt{3}}{4}$×9=$\frac{9\sqrt{3}}{4}$（当且仅当b=c时等号成立）．
故选：D．
点评 本题主要考查了余弦定理，三角形面积公式，基本不等式在解三角形中的应用，属于基本知识的考查．
练习册系列答案
相关题目
1．
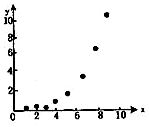如图所示的散点图，现选用两种回归模型，模型A：使用线性回归，计算相关指数$R_1^2$；模型B：用指数回归，计算出相关指数$R_2^2$，则一定有（ ）
如图所示的散点图，现选用两种回归模型，模型A：使用线性回归，计算相关指数$R_1^2$；模型B：用指数回归，计算出相关指数$R_2^2$，则一定有（ ）| A． | $R_1^2＞R_2^2$ | B． | $R_1^2＜R_2^2$ | C． | $R_1^2=R_2^2$ | D． | 无法确定 |
3．已知关于x的不等式x2-4ax+3a2＜0（a＜0）的解集为（x1，x2），则${x_1}+{x_2}+\frac{a}{{{x_1}{x_2}}}$的最大值是（ ）
| A． | $\frac{{\sqrt{6}}}{3}$ | B． | $\frac{{2\sqrt{3}}}{3}$ | C． | $\frac{{4\sqrt{3}}}{3}$ | D． | $-\frac{{4\sqrt{3}}}{3}$ |
20．在三角形ABC中，三个内角A，B，C所对的边分别为a，b，c，若acosA=bcosB，则三角形ABC一定是（ ）三角形．
| A． | 直角 | B． | 等边 | C． | 钝角 | D． | 等腰或直角 |