题目内容
1.若$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=\sqrt{2}$,($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=0,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )| A. | 30° | B. | 45° | C. | 135° | D. | 150° |
分析 根据的数量积公式计算即可.
解答 解:设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,
∵$|{\overrightarrow a}|=1$,$|{\overrightarrow b}|=\sqrt{2}$,
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=${\overrightarrow{a}}^{2}$-|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=1-$\sqrt{2}$cosθ=0,
即cosθ=$\frac{\sqrt{2}}{2}$,
∵0°≤θ≤180°,
∴θ=45°,
故选:B
点评 本题考查了向量的数量积公式的运用,属于基础题.

练习册系列答案
相关题目
11.已知集合A={x|x2-x-2≤0},B={x|log2x>1},则A∩(∁RB)=( )
| A. | (0,2] | B. | (0,2) | C. | [-1,2] | D. | (-1,2] |
9.命题“?x∈R,f(x)>0”的否定为( )
| A. | ?x0∈R,f(x0)>0 | B. | ?x∈R,f(x)<0 | C. | ?x0∈R,f(x0)≤0 | D. | ?x∈R,f(x)≤0 |
10.方程sinπx=|lnx|的解的个数是( )
| A. | 4 | B. | 8 | C. | 9 | D. | 10 |
11.一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )m3
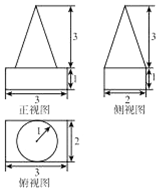

| A. | 6+π | B. | 4+π | C. | 3+π | D. | 2+π |
 发改委10月19日印发了《中国足球中长期发展规划(2016-2050年)重点任务分工》通知,其中“十三五”校园足球普及行动排名第三,为了调查重庆八中高一高二两个年级对改政策的落实情况,在每个年级随机选取20名足球爱好者,记录改政策发布后他们周平均增加的足球运动时间(单位:h),所得数据如下:
发改委10月19日印发了《中国足球中长期发展规划(2016-2050年)重点任务分工》通知,其中“十三五”校园足球普及行动排名第三,为了调查重庆八中高一高二两个年级对改政策的落实情况,在每个年级随机选取20名足球爱好者,记录改政策发布后他们周平均增加的足球运动时间(单位:h),所得数据如下: