题目内容
18.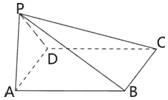 如图,平面PAD⊥平面ABCD,ABCD是边长为2的菱形,PA=PD,且∠APD=90°,∠DAB=60°.
如图,平面PAD⊥平面ABCD,ABCD是边长为2的菱形,PA=PD,且∠APD=90°,∠DAB=60°.(I)若线段PC上存在一点M,使得直线PA∥平面MBD,试确定M点的位置,并给出证明;
(II)在第(I)问的条件下,求三棱锥C-DMB的体积.
分析 (I)取线段PC的中点M,连接MD,MB,连接AC、BD相交于点O,连接OM,由三角形中位线定理可得OM∥PA,再由线面平行的判定可得PA∥平面MBD;
(II)由PA=PD,取AD中点N,可得PN⊥AD,由面面垂直的性质可得PN⊥平面ABCD,求出M到平面ABCD的距离h=$\frac{1}{2}PN=\frac{1}{2}$,然后利用等积法求得三棱锥C-DMB的体积.
解答 (I)当M为线段PC的中点时,直线PA∥平面MBD.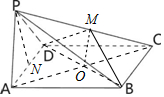
证明:取线段PC的中点M,连接MD,MB,连接AC、BD相交于点O,连接OM,
∵ABCD是菱形,∴O为AC的中点,又M为PC的中点,
∴OM∥PA,
∵OM?平面MBD,PA?平面MBD,
∴PA∥平面MBD;
(II)∵PA=PD,取AD中点N,∴PN⊥AD,
又平面PAD⊥平面ABCD,
∴PN⊥平面ABCD,
∵∠APD=90°,AD=2,PN=$\frac{1}{2}AD=1$,
又M为PC的中点,∴M到平面ABCD的距离h=$\frac{1}{2}PN=\frac{1}{2}$.
∵ABCD是边长为2的菱形,∠DAB=60°,∴${S}_{△BCD}=\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}=\sqrt{3}$.
∴${V}_{C-DMB}={V}_{M-BCD}=\frac{1}{3}{S}_{△BCD}•h=\frac{1}{3}×\sqrt{3}×\frac{1}{2}=\frac{\sqrt{3}}{6}$.
点评 本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.函数f(x)=48x-x3,x∈[-3,5]的最小值为( )
| A. | 128 | B. | -128 | C. | -117 | D. | 115 |
9.命题“?x∈R,f(x)>0”的否定为( )
| A. | ?x0∈R,f(x0)>0 | B. | ?x∈R,f(x)<0 | C. | ?x0∈R,f(x0)≤0 | D. | ?x∈R,f(x)≤0 |
3.已知关于x的不等式x2-4ax+3a2<0(a<0)的解集为(x1,x2),则${x_1}+{x_2}+\frac{a}{{{x_1}{x_2}}}$的最大值是( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $-\frac{{4\sqrt{3}}}{3}$ |
10.方程sinπx=|lnx|的解的个数是( )
| A. | 4 | B. | 8 | C. | 9 | D. | 10 |
7.函数y=$\frac{{\sqrt{{{log}_{\frac{1}{2}}}(x+1)}}}{3x+1}$的定义域是( )
| A. | [-1,+∞) | B. | (-1,+∞) | C. | $({-1,-\frac{1}{3}})∪({-\frac{1}{3},+∞})$ | D. | $({-1,-\frac{1}{3}})∪({-\frac{1}{3},0}]$ |