题目内容
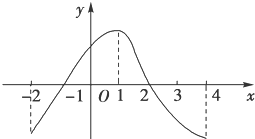 如图是函数y=f(x)的导函数的图象,给出下面四个判断.
如图是函数y=f(x)的导函数的图象,给出下面四个判断.①f(x)在区间[-2,-1]上是增函数;
②x=-1是f(x)的极小值点;
③f(x)在区间[-1,2]上是增函数,在区间[2,4]上是减函数;
④x=2是f(x)的极小值点.
其中,所有正确判断的序号是
考点:利用导数研究函数的单调性,导数的运算
专题:导数的概念及应用,导数的综合应用
分析:(1)根据导数的符号确定原函数在相应区间上的单调性,据此完成对①③的判断;
(2)极值点是导函数的变号零点,若左负右正,则是极小值点,由此判断②④的真假.
(2)极值点是导函数的变号零点,若左负右正,则是极小值点,由此判断②④的真假.
解答:
解:观察图象可知,导函数在[-2,-1]上为负,在[-1,2]上为正,[2,4]上为负,
所以原函数的增区间为[-1,2],减区间为[-2,-1],[2,4].所以①错;③对;
又f′(-1)=0,且x=-1左边导数为负,右边导数为正,所以x=-1是极小值点,故②对;
因为f′(2)=0,且x=2左边导数为正,右边导数为负,所以x=2是极大值点,故④错.
故答案为②③.
所以原函数的增区间为[-1,2],减区间为[-2,-1],[2,4].所以①错;③对;
又f′(-1)=0,且x=-1左边导数为负,右边导数为正,所以x=-1是极小值点,故②对;
因为f′(2)=0,且x=2左边导数为正,右边导数为负,所以x=2是极大值点,故④错.
故答案为②③.
点评:本题考查了导函数与原函数的关系,一般来说,研究原函数的单调性要看导数的符号,而极值点则是原函数的变号零点,据此进行判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知a∈R,则“a≤2”是“|x-2|-|x|>a有解”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
(理)直平行六面体ABCD-A1B1C1D1的棱长均为2,∠BAD=60°,则对角线A1C与侧面D1C1CD所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
{an}和{bn},其前n项和分别为Sn,Tn,且
=
,则
等于( )
| Sn |
| Tn |
| 7n+2 |
| n+3 |
| a2+a20 |
| b2+b20 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是某校教学楼的楼梯(部分),如果每个台阶的高10cm,宽15cm,那么楼梯的坡度i=( )


A、
| ||
B、
| ||
C、
| ||
D、
|