题目内容
{an}和{bn},其前n项和分别为Sn,Tn,且
=
,则
等于( )
| Sn |
| Tn |
| 7n+2 |
| n+3 |
| a2+a20 |
| b2+b20 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:利用等差数列的性质可得
=
,即可求得结论.
| a2+a20 |
| b2+b20 |
| S21 |
| T21 |
解答:
解:
=
=
=
=
=
.
故选D.
| a2+a20 |
| b2+b20 |
| a1+a21 |
| b1+b21 |
| ||
|
| s21 |
| T21 |
| 7×21+2 |
| 21+3 |
| 149 |
| 24 |
故选D.
点评:本题主要考查等差数列的性质及前n项和公式的应用,考查学生灵活运用公式的能力及运算求解能力,属基础题.

练习册系列答案
相关题目
已知π<θ<3π,则
化简为( )
|
A、sin
| ||
B、cos
| ||
C、-sin
| ||
D、-cos
|
log2210=( )
| A、5 | B、-5 | C、10 | D、-10 |
(文)在正方体ABCD-A1B1C1D1中,与AD1成45°角的棱的条数是( )
| A、4条 | B、6条 | C、8条 | D、10条 |
过双曲线
-
=1(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若
=
,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| 1 |
| 2 |
| BC |
| A、3x±y=0 |
| B、x±3y=0 |
| C、2x±y=0 |
| D、x±2y=0 |
在平行四边形ABCD中,
+
-
等于( )
| BC |
| CD |
| AD |
A、
| ||
B、
| ||
C、
| ||
D、
|
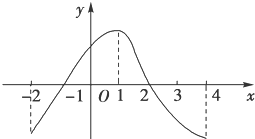 如图是函数y=f(x)的导函数的图象,给出下面四个判断.
如图是函数y=f(x)的导函数的图象,给出下面四个判断.