题目内容
已知a∈R,则“a≤2”是“|x-2|-|x|>a有解”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:不等式的解法及应用
分析:先求出|x-2|-|x|>a有解的a的取值范围:a<2,然后判断a≤2和a<2的关系即可.
解答:
解:∵|x-2|-|x|≤|x-2-x|=2,∴若|x-2|-|x|>a有解,只要|x-2|-|x|的最大值大于a,即2>a,即<2;
∴a≤2不一定得到a<2,即“a≤2“不是“|x-2|-|x|>a“的充分条件;
而a<2一定能得到a≤2,∴“a≤2“是“|x-2|-|x|>a“的必要条件;
∴“a≤2“是“|x-2|-|x|>a“的必要不充分条件.
故选B.
∴a≤2不一定得到a<2,即“a≤2“不是“|x-2|-|x|>a“的充分条件;
而a<2一定能得到a≤2,∴“a≤2“是“|x-2|-|x|>a“的必要条件;
∴“a≤2“是“|x-2|-|x|>a“的必要不充分条件.
故选B.
点评:考查绝对值不等式的一个性质:|a|-|b|≤|a-b|,以及充分条件,必要条件,必要不充分条件的概念.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知复数z满足(1+i)z=i,则z=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
log2210=( )
| A、5 | B、-5 | C、10 | D、-10 |
下列命题正确的是( )
A、若
| ||||||||||||
B、
| ||||||||||||
C、若
| ||||||||||||
D、
|
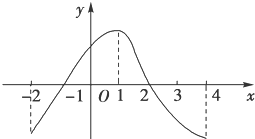 如图是函数y=f(x)的导函数的图象,给出下面四个判断.
如图是函数y=f(x)的导函数的图象,给出下面四个判断.