题目内容
在平面内,余弦定理给出了三角形的三条边与其中一个角的关系,如:a2=b2+c2-2bccosA,把四面体V-BCD与三角形作类比,设二面角V-BC-D,V-CD-B,V-BD-C,C-VB-D,B-VC-D,B-VD-C的大小依次为α1,α2,α3,β1,β2,β3我们可以得到“四面体的余弦定理”: .(只需写出一个关系式)
考点:类比推理
专题:规律型,推理和证明
分析:这是一个类比推理的题,在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,
解答:
解:由已知在平面内,余弦定理给出了三角形的三条边与其中一个角的关系,如:a2=b2+c2-2bccosA,把四面体V-BCD与三角形作类比,设二面角V-BC-D,V-CD-B,V-BD-C,C-VB-D,B-VC-D,B-VD-C的大小依次为α1,α2,α3,β1,β2,β3我们可以得到“四面体的余弦定理”:
S2△BCD=S2△VBC+S2△VCD+S2△VBD-2S△VBCS△VCDcosβ2-2S△VCDS△VBDcosβ3-2S△VBCS△VBDcosβ1.
故答案为:S2△BCD=S2△VBC+S2△VCD+S2△VBD-2S△VBCS△VCDcosβ2-2S△VCDS△VBDcosβ3-2S△VBCS△VBDcosβ1.
S2△BCD=S2△VBC+S2△VCD+S2△VBD-2S△VBCS△VCDcosβ2-2S△VCDS△VBDcosβ3-2S△VBCS△VBDcosβ1.
故答案为:S2△BCD=S2△VBC+S2△VCD+S2△VBD-2S△VBCS△VCDcosβ2-2S△VCDS△VBDcosβ3-2S△VBCS△VBDcosβ1.
点评:主要是考查了类比推理的运用,属于中档题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目

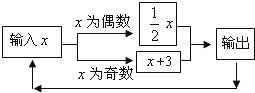
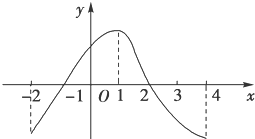 如图是函数y=f(x)的导函数的图象,给出下面四个判断.
如图是函数y=f(x)的导函数的图象,给出下面四个判断.