题目内容
如图是某校教学楼的楼梯(部分),如果每个台阶的高10cm,宽15cm,那么楼梯的坡度i=( )


A、
| ||
B、
| ||
C、
| ||
D、
|
考点:解三角形
专题:计算题,解三角形
分析:坡度=垂直距离:水平距离.仔细观察可得:所有台阶的高的和(10×6=60cm)即为AC的长,所有台阶宽的和(15×6=90cm)即为BC的长.
解答:
解:由题意,AC=10×6=60cm,BC=15×6=90cm,
∴tanB=
=
.
故选D.
∴tanB=
| AC |
| BC |
| 2 |
| 3 |
故选D.
点评:此题主要考查学生对直角三角形的坡度坡角的掌握情况情况.此题的关键是明白台阶的高的和等于楼梯的铅直高度,台阶的宽的和等于楼梯的水平长度.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
(文)在正方体ABCD-A1B1C1D1中,与AD1成45°角的棱的条数是( )
| A、4条 | B、6条 | C、8条 | D、10条 |
过双曲线
-
=1(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B,C.若
=
,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| 1 |
| 2 |
| BC |
| A、3x±y=0 |
| B、x±3y=0 |
| C、2x±y=0 |
| D、x±2y=0 |
设直线AB的方程为(a-3)x+y+2-a=0,若直线AB不经过第二象限,则a的取值范围为( )
| A、a≤1 | B、a≤3 |
| C、a≤2 | D、a<3 |
下列命题正确的是( )
A、若
| ||||||||||||
B、
| ||||||||||||
C、若
| ||||||||||||
D、
|
已知函数y=
,则y′等于( )
| sin2x |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
在平行四边形ABCD中,
+
-
等于( )
| BC |
| CD |
| AD |
A、
| ||
B、
| ||
C、
| ||
D、
|
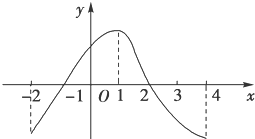 如图是函数y=f(x)的导函数的图象,给出下面四个判断.
如图是函数y=f(x)的导函数的图象,给出下面四个判断.