题目内容
已知D为△ABC的边BC的中点,△ABC所在平面内有一点P,满足
+
+
=0,则
的值为 .
| PA |
| BP |
| CP |
| |AP| |
| |PD| |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:由于D为△ABC的边BC的中点,可得
+
=2
.由于满足
+
+
=
,可得
=2
.即可得出.
| PB |
| PC |
| PD |
| PA |
| BP |
| CP |
| 0 |
| PA |
| PD |
解答:
解:∵D为△ABC的边BC的中点,
∴
+
=2
.
∵满足
+
+
=
,
∴
=2
.
∴
=2.
故答案为:2.
∴
| PB |
| PC |
| PD |
∵满足
| PA |
| BP |
| CP |
| 0 |
∴
| PA |
| PD |
∴
| |AP| |
| |PD| |
故答案为:2.
点评:本题考查了向量的平行四边形法则、向量的共线与线性运算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,在 ABCD中,点E是AB的中点,若
=
,
=
,则
=( )

| AB |
| a |
| AD |
| b |
| EC |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知π<θ<3π,则
化简为( )
|
A、sin
| ||
B、cos
| ||
C、-sin
| ||
D、-cos
|
设直线AB的方程为(a-3)x+y+2-a=0,若直线AB不经过第二象限,则a的取值范围为( )
| A、a≤1 | B、a≤3 |
| C、a≤2 | D、a<3 |
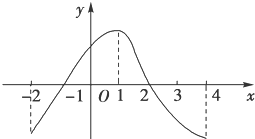 如图是函数y=f(x)的导函数的图象,给出下面四个判断.
如图是函数y=f(x)的导函数的图象,给出下面四个判断.