题目内容
(理)直平行六面体ABCD-A1B1C1D1的棱长均为2,∠BAD=60°,则对角线A1C与侧面D1C1CD所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与平面所成的角
专题:空间角
分析:作A1E⊥C1D1,垂足为E,则可得对角线A1C与侧面DCC1D1所成角,从而可求对角线A1C与侧面DCC1D1所成角的正弦值.
解答:
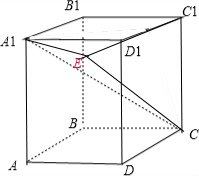 解:作A1E⊥C1D1,垂足为E,连CE,A1E,A1C.
解:作A1E⊥C1D1,垂足为E,连CE,A1E,A1C.
∵ABCD-A1B1C1D1是直平行六面体
∴A1E⊥平面DCC1D1,
∴∠A1CE就是对角线A1C与侧面DCC1D1所成角
∵CE?平面A1B1C1D1,
∴A1E⊥CE
∵棱长都为2的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,
∴A1E=2sin60°=
,D1E=1,
∴A1C1=2
,∴A1C=4,
∴CE=
,
在Rt△A1EC中,sin∠A1CE=
=
.
故选:A.
 解:作A1E⊥C1D1,垂足为E,连CE,A1E,A1C.
解:作A1E⊥C1D1,垂足为E,连CE,A1E,A1C.∵ABCD-A1B1C1D1是直平行六面体
∴A1E⊥平面DCC1D1,
∴∠A1CE就是对角线A1C与侧面DCC1D1所成角
∵CE?平面A1B1C1D1,
∴A1E⊥CE
∵棱长都为2的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,
∴A1E=2sin60°=
| 3 |
∴A1C1=2
| 3 |
∴CE=
| 13 |
在Rt△A1EC中,sin∠A1CE=
| A1E |
| A1C |
| ||
| 4 |
故选:A.
点评:本题重点考查线面角,解题的关键是利用线面垂直,作出线面角,属于中档题.

练习册系列答案
相关题目
如图,在 ABCD中,点E是AB的中点,若
=
,
=
,则
=( )

| AB |
| a |
| AD |
| b |
| EC |

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知π<θ<3π,则
化简为( )
|
A、sin
| ||
B、cos
| ||
C、-sin
| ||
D、-cos
|
(文)在正方体ABCD-A1B1C1D1中,与AD1成45°角的棱的条数是( )
| A、4条 | B、6条 | C、8条 | D、10条 |
已知函数y=
,则y′等于( )
| sin2x |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
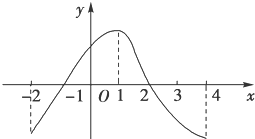 如图是函数y=f(x)的导函数的图象,给出下面四个判断.
如图是函数y=f(x)的导函数的图象,给出下面四个判断.