题目内容
在直角坐标系xOy中,过椭圆
(φ为参数)的右焦点,斜率为
的直线方程为 .
|
| 1 |
| 2 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:由椭圆
(φ为参数)消去参数φ化为直角坐标方程:
+y2=1.可得c=
=
=2
,得右焦点F(2
,0),再利用点斜式即可得出所求的直线方程.
|
| x2 |
| 25 |
| a2-b2 |
| 25-1 |
| 6 |
| 6 |
解答:
解:由椭圆
(φ为参数)消去参数φ化为直角坐标方程:
+y2=1.
∴c=
=
=2
,得右焦点F(2
,0),
故所求的直线方程为:y=
(x-2
),化为x-2y-2
=0.
故答案为:x-2y-2
=0.
|
| x2 |
| 25 |
∴c=
| a2-b2 |
| 25-1 |
| 6 |
| 6 |
故所求的直线方程为:y=
| 1 |
| 2 |
| 6 |
| 6 |
故答案为:x-2y-2
| 6 |
点评:本题考查了椭圆的参数方程化为直角坐标方程、直线的点斜式,属于基础题.

练习册系列答案
相关题目
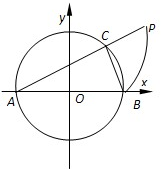 如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )
如图,在直角坐标系xoy中,AB是半圆O:x2+y2=1(y≥0)的直径,点C是半圆O上任一点,延长AC到点P,使CP=CB,当点C从点B运动到点A时,动点P的轨迹的长度是( )| A、2π | ||
B、
| ||
| C、π | ||
D、4
|
曲线y=x-
在点(1,0)处的切线方程为( )
| 1 |
| x |
| A、y=2x-2 |
| B、y=x-1 |
| C、y=0 |
| D、y=-x+1 |
 如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD=
如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD= 在边长为10的正方形ABCD内有一动点P,AP=9,作PQ⊥BC于Q,PR⊥CD于R,求矩形PQCR面积的最小值和最大值,并指出取最大值时P的具体位置.
在边长为10的正方形ABCD内有一动点P,AP=9,作PQ⊥BC于Q,PR⊥CD于R,求矩形PQCR面积的最小值和最大值,并指出取最大值时P的具体位置.