题目内容
(坐标系与参数方程选做题)在直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:
(θ为参数)和曲线C2:ρ=2
cos(θ+
)上,则|AB|的最小值为 .
|
| 2 |
| π |
| 4 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把曲线C1,C2的方程分别化为直角坐标方程,则曲线C1,C2上的两点A,B|AB|的最小值=|C1C2|-R-r=
-
-1.
| (4-1)2+1 |
| 2 |
解答:
解:由曲线C1:
(θ为参数)化为(x-4)2+y2=1,得到圆心C1(4,0),半径r=1;
由曲线C2:ρ=2
cos(θ+
)展开可得:ρ2=2
ρ(
cosθ-
sinθ),
即为x2+y2=2x-2y,化为(x-1)2+(y+1)2=2,圆心C2(1,1),半径R=
.
由于点A,B分别在曲线C1,C2上.
∴|AB|的最小值=|C1C2|-R-r=
-
-1=
-
-1.
故答案为:
-
-1.
|
由曲线C2:ρ=2
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
即为x2+y2=2x-2y,化为(x-1)2+(y+1)2=2,圆心C2(1,1),半径R=
| 2 |
由于点A,B分别在曲线C1,C2上.
∴|AB|的最小值=|C1C2|-R-r=
| (4-1)2+1 |
| 2 |
| 10 |
| 2 |
故答案为:
| 10 |
| 2 |
点评:本题考查了把曲线的参数方程和极坐标方程化为直角坐标方程、求两条曲线的最小距离,属于基础题.

练习册系列答案
相关题目
函数f(x)=2x2-kx-8在区间[1,2]上不单调,则实数k的取值范围为( )
| A、[4,8] |
| B、(-∞,4]∪[8,+∞) |
| C、(-∞,4)∪(8,+∞) |
| D、(4,8) |
cos(-
)的值等于( )
| 5π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
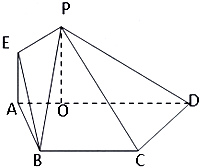 如图,在等腰梯形ABCD中,AD∥BC,
如图,在等腰梯形ABCD中,AD∥BC,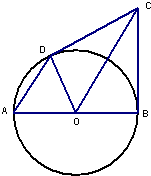 (几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD=
(几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD=