题目内容
设x,y满足约束条件
,若目标函数z=(
+
)x+y(a>0,b>0)的最大值为8,则a+2b的最小值为 .
|
| 2 |
| a |
| 1 |
| b |
考点:简单线性规划的应用
专题:数形结合法,不等式的解法及应用
分析:作出可行域,利用目标函数z=(
+
)x+y(a>0,b>0)在(1,4)处取得最大值为8,可得
+
=4,利用“1”的代换,结合基本不等式,即可求a+2b的最小值.
| 2 |
| a |
| 1 |
| b |
| 2 |
| a |
| 1 |
| b |
解答:
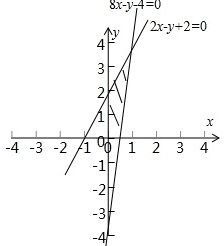 解:满足约束条件
解:满足约束条件
的可行域,如图所示,
四边形的四个顶点坐标分别为(0,0),(0,2),(1,4),(0.5,0),
由题意,目标函数z=(
+
)x+y(a>0,b>0)在(1,4)处取得最大值为8,
∴
+
=4,
∴a+2b=
(a+2b)(
+
)=
(4+
+
)≥
(4+2
)=2,
当且仅当
=
时,取等号,
∴a+2b的最小值为2.
故答案为:2.
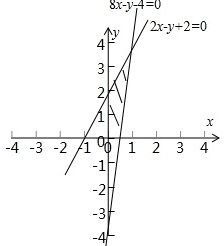 解:满足约束条件
解:满足约束条件
|
四边形的四个顶点坐标分别为(0,0),(0,2),(1,4),(0.5,0),
由题意,目标函数z=(
| 2 |
| a |
| 1 |
| b |
∴
| 2 |
| a |
| 1 |
| b |
∴a+2b=
| 1 |
| 4 |
| 2 |
| a |
| 1 |
| b |
| 1 |
| 4 |
| a |
| b |
| 4b |
| a |
| 1 |
| 4 |
|
当且仅当
| a |
| b |
| 4b |
| a |
∴a+2b的最小值为2.
故答案为:2.
点评:本题考查线性规划知识的运用,考查基本不等式,考查学生的计算能力,考查数形结合的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
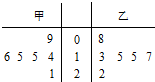 甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,x1,x2分别表示甲乙两名运动员这项测试成绩的众数,s1,s2分别表示甲乙两名运动员这项测试成绩的标准差,则有( )
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,x1,x2分别表示甲乙两名运动员这项测试成绩的众数,s1,s2分别表示甲乙两名运动员这项测试成绩的标准差,则有( )| A、x1>x2,s1<s2 |
| B、x1=x2,s1<s2 |
| C、x1=x2,s1=s2 |
| D、x1=x2,s1>s2 |
数列{an}中a1=1,a5=13,an+2+an=2an+1;数列{bn}中,b2=6,b3=3,bn+2bn=b
,在直角坐标平面内,已知点列P1(a1,b1),P2(a2,b2),P3(a3,b3),…,Pn(an,bn)…,则向量
+
+
+…+
的坐标为( )
2 n+1 |
| P1P2 |
| P3P4 |
| P5P6 |
| P2009P2010 |
A、(3015,8[(
| ||
B、(3012,8[(
| ||
C、(3015,8[(
| ||
D、(3018,8[(
|
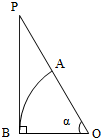 如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧
如图,直角△POB中,∠PBO=90°,以O为圆心、OB为半径作圆弧交OP于A点.若圆弧