题目内容
【坐标系与参数方程选做题】
在极坐标系ρOθ(ρ≥0,0≤θ<2π)中,点A(2,
)关于直线l:ρcosθ=1的对称点的极坐标为 .
在极坐标系ρOθ(ρ≥0,0≤θ<2π)中,点A(2,
| π |
| 2 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:设A(2,
)关于直线l:ρcosθ=1的对称点为B(ρ,θ),则OA=AB=2,且OA⊥AB.从而OB=2
,∠AOB=
即可得出.
| π |
| 2 |
| 2 |
| π |
| 4 |
解答:
 解:如图,在极坐标系ρOθ(ρ≥0,0≤θ<2π)中,
解:如图,在极坐标系ρOθ(ρ≥0,0≤θ<2π)中,
设A(2,
)关于直线l:ρcosθ=1的对称点为B(ρ,θ),
则OA=AB=2,且OA⊥AB.
从而OB=2
,∠AOB=
,
即ρ=2
,θ=
-
=
.
故答案为:(2
,
).
 解:如图,在极坐标系ρOθ(ρ≥0,0≤θ<2π)中,
解:如图,在极坐标系ρOθ(ρ≥0,0≤θ<2π)中,设A(2,
| π |
| 2 |
则OA=AB=2,且OA⊥AB.
从而OB=2
| 2 |
| π |
| 4 |
即ρ=2
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
故答案为:(2
| 2 |
| π |
| 4 |
点评:本题考查了极坐标系下的对称点的坐标求法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=2x2-kx-8在区间[1,2]上不单调,则实数k的取值范围为( )
| A、[4,8] |
| B、(-∞,4]∪[8,+∞) |
| C、(-∞,4)∪(8,+∞) |
| D、(4,8) |
一个三棱柱的侧棱垂直于底面,且所有棱长都为a,则此三棱柱的外接球的表面积为( )
| A、πa2 | ||
| B、15πa2 | ||
C、
| ||
D、
|
cos(-
)的值等于( )
| 5π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为
,则
的值为( )
| 1 |
| 3 |
| AD |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
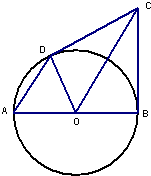 (几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD=
(几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD= 已知函数f(x)=lg(2+x)+lg(2-x).
已知函数f(x)=lg(2+x)+lg(2-x).